Your next great Lessn starts here.

Today’s Adventure: Putting Fractions in Order! – What are fractions? – Fractions represent parts of a whole. – Visualizing fractions – Use fraction bars or circles to see size differences. – Importance of ordering – Ordering helps in fair sharing and understanding math problems. – Methods to compare fractions – Compare using common denominators or numerators. | Begin the lesson by explaining the concept of fractions as parts of a whole, ensuring students understand the terms numerator and denominator. Introduce visual aids like fraction bars or pie charts to help them compare sizes. Discuss real-life scenarios where ordering fractions is necessary, such as dividing a pizza among friends or measuring ingredients for a recipe. Teach different methods to order fractions, such as finding a common denominator or comparing numerators when denominators are the same. Encourage students to practice by providing examples and guiding them through the process of ordering fractions from least to greatest or vice versa.

Understanding Fractions – A fraction represents part of a whole – Consists of numerator over denominator – Examples: 1/2, 3/4, 2/3 – 1/2 is half, 3/4 is three quarters, 2/3 is two thirds – Visualize fractions with pie charts – Pie charts show fractions as parts of a circle | Begin the lesson by explaining that a fraction represents a part of a whole, which is a concept they encounter in everyday life, such as slicing a pizza or sharing candy. The numerator (top number) indicates how many parts we have, while the denominator (bottom number) shows the total number of equal parts the whole is divided into. Provide visual aids like pie charts or fraction bars to help students visualize fractions. This will set the foundation for understanding how to compare and order fractions later in the lesson. Encourage students to think of their own examples of fractions from daily life to make the concept more relatable.

Putting Fractions in Order – Comparing fractions by size – Numerator size can be deceiving – A fraction with a larger numerator is not necessarily larger. Compare 3/4 and 4/5. – Using common denominators – Find a common denominator to compare fractions like 2/3 and 3/4. – Ordering fractions correctly – Practice by arranging fractions from smallest to largest. | This slide introduces the concept of comparing and ordering fractions. Start by explaining that fractions represent parts of a whole and can be compared by their size. Emphasize that a bigger numerator does not always mean a bigger fraction, using examples to illustrate this common misconception. Teach students how to find a common denominator to compare fractions effectively. Finally, engage the class with an activity where they practice putting a set of fractions in order from smallest to largest, reinforcing the concept that fractions with different numerators and denominators can be compared by converting them to have the same denominator.

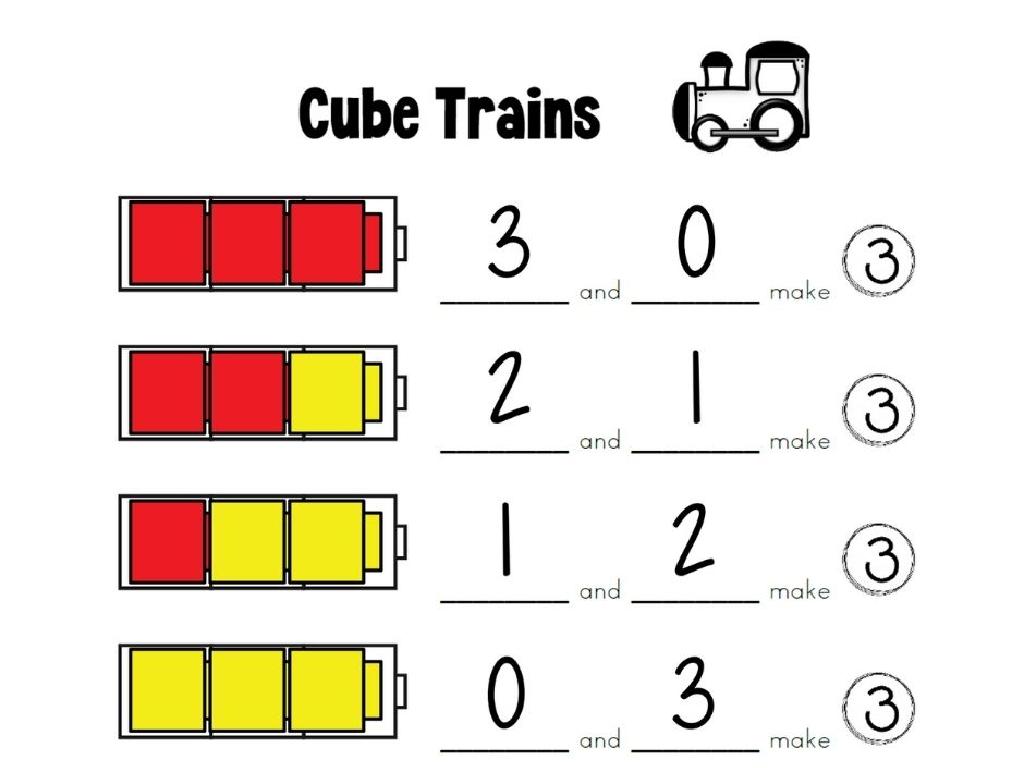
Ordering Fractions with Same Denominators – Compare numerators directly – Larger numerator means larger fraction – Example: 3/8, 7/8, 1/8 – Which is smallest or largest: 3/8, 7/8, or 1/8? – Arrange from smallest to largest – 1/8 < 3/8 < 7/8 | This slide is focused on teaching students how to order fractions that have the same denominator. Start by explaining that when fractions have the same bottom number (denominator), they have equal-sized parts. To find out which is larger or smaller, they only need to look at the top numbers (numerators). The fraction with the larger numerator is the larger fraction because it represents more parts of the whole. Use the example provided to illustrate this concept by showing that 1/8 is smaller than 3/8, which is smaller than 7/8. Have students practice by providing additional sets of fractions with the same denominators and asking them to order them from smallest to largest.

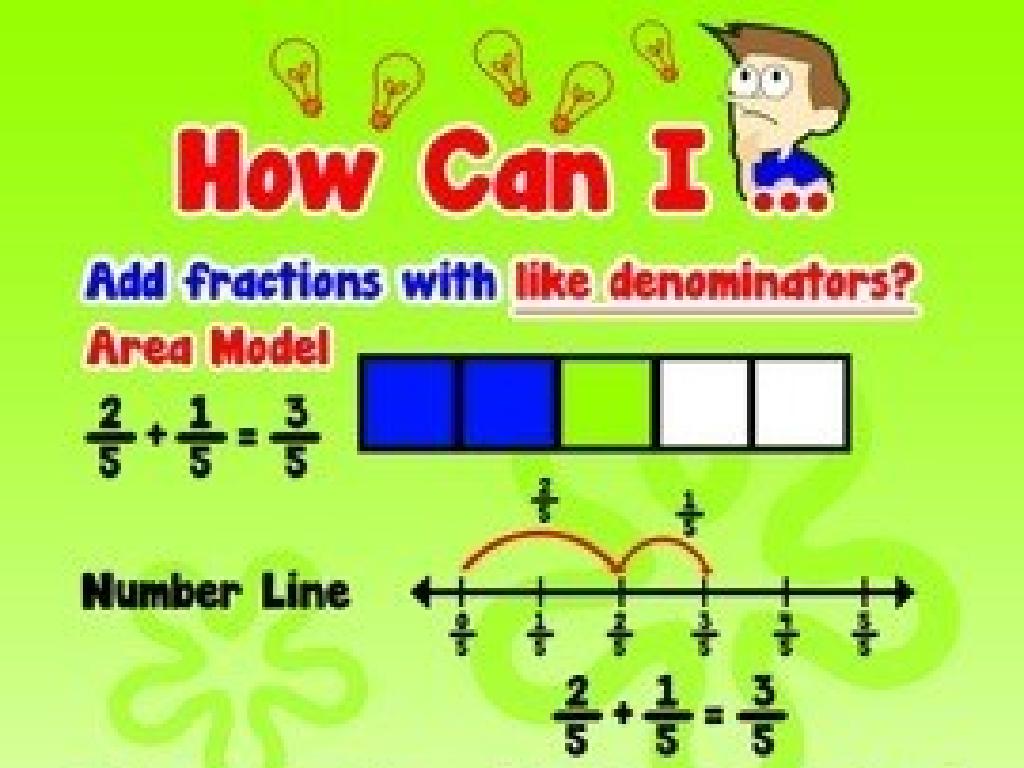
Ordering Fractions with Different Denominators – Find a common denominator – A number that all denominators can divide into – Convert to same denominator – Make equivalent fractions with common denominator – Example: 1/2, 3/8, 4/5 – Convert 1/2, 3/8, 4/5 to 4/8, 3/8, 8/10 – Arrange fractions in order – Place in order from smallest to largest | This slide introduces the concept of ordering fractions by finding a common denominator. Start by explaining that a common denominator is a shared multiple of the original denominators. Show how to convert each fraction to an equivalent fraction with this common denominator. Use the example provided to illustrate the process: convert 1/2, 3/8, and 4/5 to 4/8, 3/8, and 8/10 respectively. Once converted, guide students to compare the numerators and arrange the fractions in ascending order. Emphasize the importance of this skill in real-life situations, such as comparing amounts or portions. Encourage students to practice with additional examples.

Using Benchmarks to Order Fractions – Benchmarks: 0, 1/2, and 1 – Compare fractions to benchmarks – Is the fraction less, equal, or greater than 1/2? – Determine fraction’s relation to benchmark – Example: 3/4 > 1/2, so it’s closer to 1 – Order fractions using benchmarks – Arrange fractions based on their benchmark comparison | This slide introduces the concept of using benchmarks to order fractions. Benchmarks are standard points of reference that students can use to compare and order fractions. Start by explaining what benchmarks are and how they can be used as a tool for comparison. Then, guide students through the process of deciding whether a fraction is less than, equal to, or greater than a given benchmark. Use examples to illustrate how to place fractions in order relative to the benchmark. For instance, if a fraction is greater than 1/2 but less than 1, it would be placed between these two benchmarks. Encourage students to practice with different sets of fractions and benchmarks to become comfortable with this method.

Let’s Practice Together: Ordering Fractions – Find common denominators – Convert to equivalent fractions – Use multiples to find a common base for all fractions – Order from least to greatest – Arrange fractions based on their numerators – Example: 1/4, 2/3, 5/6 – Smallest to largest: 1/4 < 2/3 < 5/6 after conversion | This slide is a class activity designed to help students practice putting fractions in order. Start by explaining the concept of common denominators and how to find them. Then, guide students through the process of converting fractions to have the same denominator so they can be easily compared. Once converted, students should arrange the fractions from the smallest to the largest. Use the example provided to walk through the steps together. For the activity, students can work individually or in groups to find common denominators for different sets of fractions and order them. Encourage students to explain their reasoning and the steps they took to arrive at their answers.

Class Activity: Fraction Ordering Race – Pair up for the race – Order the set of fractions – Arrange fractions from smallest to largest – Find common denominators – Use equivalent fractions to compare – Win a prize for finishing first! | This activity is designed to reinforce the concept of ordering fractions by finding common denominators. Students will work in pairs to encourage collaboration. Provide each pair with a set of fractions to order. Remind them to use the methods learned in class to find equivalent fractions with common denominators, which will make it easier to compare and order them. The first pair to correctly arrange their fractions from smallest to largest wins a small prize. This competitive element will engage students and make the learning process fun. Possible variations of the activity could include ordering fractions from largest to smallest, using mixed numbers, or including improper fractions.

Conclusion & Homework: Ordering Fractions – Congratulations on learning to order fractions! – Review the ordering steps we practiced – Recall finding common denominators and comparing numerators – Complete the ‘Order the Fractions’ worksheet – Worksheet has sets of fractions to put in order – Be ready to discuss your answers | Students have done a great job learning how to put fractions in order. It’s important for them to remember the steps we’ve practiced in class, such as finding common denominators and comparing numerators to determine the order of fractions. For homework, they are assigned a worksheet that will provide additional practice with a variety of fractions to order. This will help reinforce today’s lesson and prepare them for the next class where we will review their answers and address any questions. Encourage students to try their best and remind them that making mistakes is a part of learning.