Your next great Lessn starts here.

Exploring Distance on the Coordinate Plane – Understanding the coordinate plane – A grid with horizontal (x-axis) and vertical (y-axis) lines – Defining a point – A location on the plane represented by (x, y) – Calculating distance between points – Use the distance formula: ((x2 – x1)² + (y2 – y1)²) – Practical applications of distance – Measure lengths and paths in real-world scenarios | This slide introduces students to the fundamental concepts of coordinate geometry, focusing on the coordinate plane and the concept of a point. Students will learn how to calculate the distance between two points using the distance formula, which is derived from the Pythagorean theorem. Emphasize the importance of understanding the axes and how each point is an ordered pair of numbers. Provide examples of how this knowledge is applied in real life, such as in navigation, architecture, and game design. Encourage students to practice by plotting points and calculating distances between them.

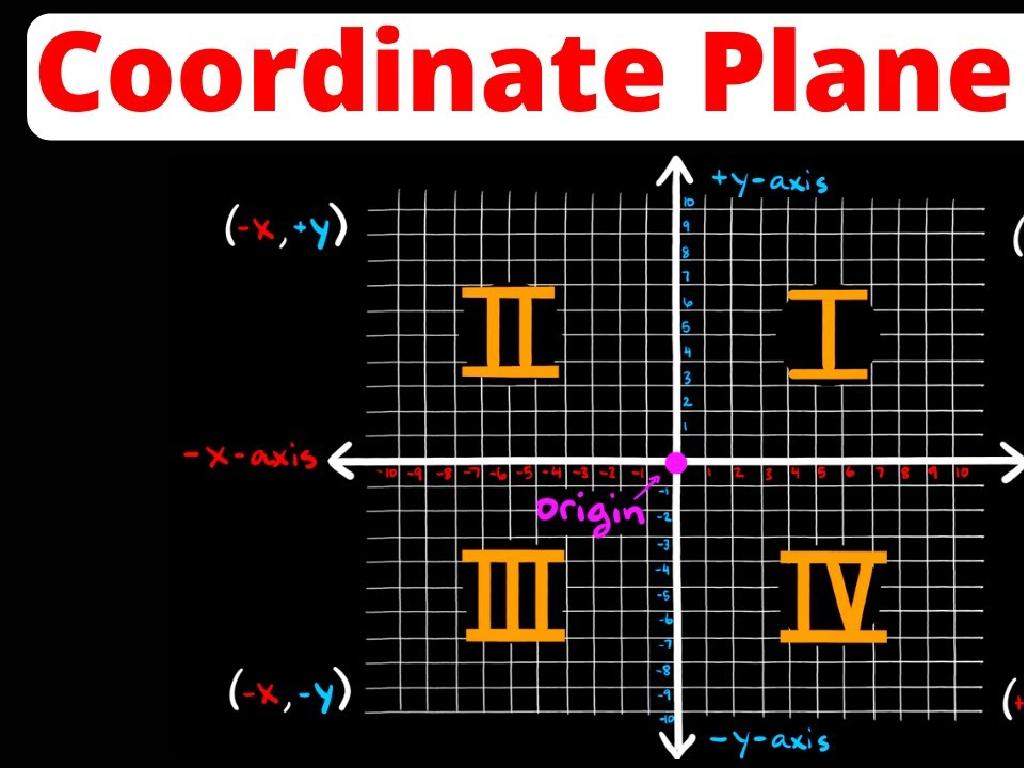
Exploring the Coordinate Plane – Define the coordinate plane – A two-dimensional surface for graphing points, lines, and curves. – Understand the X and Y axes – X-axis is horizontal, Y-axis is vertical, intersecting at the origin. – Origin: The (0,0) starting point – The center of the plane where the X and Y axes cross. – Plotting points on the plane – Each point is defined by an (x,y) pair showing its position. | Introduce the concept of the coordinate plane as the foundation for graphing in mathematics. Explain that it consists of two perpendicular lines called axes, with the horizontal line known as the X-axis and the vertical line as the Y-axis. The point where they intersect is called the origin, which has coordinates (0,0). Emphasize the importance of the origin as a reference point for all other points on the plane. Demonstrate how to plot points by using their x (horizontal) and y (vertical) coordinates, and ensure students understand that every point on the plane is represented by a unique pair of numbers.

Plotting Points on the Coordinate Plane – How to plot X and Y coordinates – Locate X on the horizontal, Y on the vertical axis – Example: Plot (3, 4) and (-2, -1) – Start at origin (0,0), move right 3, up 4 for (3, 4); left 2, down 1 for (-2, -1) – Student practice on grid – Use your grid to plot points given by the teacher | This slide introduces students to the concept of plotting points on a coordinate plane. Begin by explaining the X (horizontal) and Y (vertical) axes and how each point is defined by an (X, Y) coordinate pair. Use the example to demonstrate moving along the axes to plot the points (3, 4) and (-2, -1). For the practice activity, provide students with a list of points to plot on their own coordinate grids. This will help solidify their understanding of positive and negative values on both axes. Encourage students to check each other’s work for accuracy. This hands-on activity is crucial for their understanding of the coordinate plane and will be foundational for learning how to calculate the distance between two points.

Understanding Distance on a Coordinate Plane – Define distance concept – Distance is the length between two points. – Measure straight line distance – Use a ruler to measure the length directly. – Distance on the coordinate plane – Plot points on a grid and find the length between them. – Apply distance formula – Use the formula ((x2-x1)² + (y2-y1)²) to calculate distance. | This slide introduces the concept of distance in the context of mathematics and specifically on a coordinate plane. Begin by defining distance as the amount of space between two points. Show how to measure the distance in a straight line using a ruler for simple cases. Then, transition to the coordinate plane, explaining how to plot points and visualize the distance between them on the grid. Finally, introduce the distance formula as a method to calculate the exact distance between two points on the plane. Provide examples and encourage students to practice plotting points and using the formula to reinforce the concept.

The Distance Formula on the Coordinate Plane – Introduction to the Distance Formula – Distance Formula: [(x2 – x1)² + (y2 – y1)²] – The formula calculates the distance between two points (x1, y1) and (x2, y2). – Break down the formula step by step – Understand each part: subtract coordinates, square the result, add squares, then square root. – Practice with an example – Example: Find the distance between (3, 4) and (6, 8). | This slide introduces the Distance Formula, a key concept in understanding the coordinate plane. The formula is rooted in the Pythagorean theorem and is used to calculate the straight-line distance between two points in a plane. Start by explaining the notation and what each part of the formula represents. Then, break down the formula into manageable steps, explaining the order of operations. Finally, provide a clear example, such as finding the distance between (3, 4) and (6, 8), and walk through each step of the formula to ensure students grasp the concept. Encourage students to practice with additional points to solidify their understanding.

Applying the Distance Formula – Example: Points (3, 4) & (-2, -1) – Step-by-step distance calculation – Subtract x-values and y-values, then square the results – Use the formula: ((x2-x1)² + (y2-y1)²) – Square root of sum gives the distance – Verify with a ruler on a grid – Ensure calculation matches the actual measurement | This slide is aimed at teaching students how to apply the distance formula to calculate the distance between two points on a coordinate plane. Start with an example using the points (3, 4) and (-2, -1). Walk the students through the process of subtracting and squaring the x and y values of the points, then summing these squares. Emphasize the importance of the order of operations when performing these calculations. After finding the sum, demonstrate how to find the square root to get the distance. Finally, show students how to check their work by measuring the distance between the points on a grid with a ruler. This reinforces the concept and shows the practical application of the formula. Encourage students to practice with different points to gain confidence in using the distance formula.

Class Activity: Calculating Distance – Problem 1: Points (5, 5) & (1, 2) – Use the distance formula to solve – Problem 2: Points (-3, -4) & (0, 0) – Apply the formula to find distance from origin – Work independently on problems – Teacher provides assistance | This slide presents two practice problems to help students apply the distance formula. For Problem 1, students will calculate the distance between the points (5, 5) and (1, 2) using the distance formula ((x2 – x1)² + (y2 – y1)²). For Problem 2, they will find the distance of the point (-3, -4) from the origin (0, 0), which is a special case of the distance formula. Encourage students to work independently to solve these problems, reinforcing their understanding of the coordinate plane and the concept of distance. The teacher should circulate the room, providing assistance and ensuring that students are correctly applying the formula. Possible variations for different students could include finding the distance between two points with one or both points having the same x or y values, or finding the distance between points in different quadrants.

Real-World Application of Distance Formula – Distance formula in daily life Used to calculate space between two locations – GPS technology uses distance GPS calculates how far you are from a destination – Mapping relies on accurate distances Maps use it to give precise directions – Discuss other applications | This slide aims to show students the practical applications of the distance formula beyond the classroom. Highlight how the distance formula is essential in technologies like GPS, which they may use regularly. Explain that GPS systems calculate the shortest path between two points, which is a direct application of the distance formula. Mapping services also use this formula to provide accurate travel directions. Encourage students to think about other areas where measuring exact distances might be important, such as in architecture, sports, or even video game design. This discussion can help them appreciate the relevance of math in everyday life and various professions.

Class Activity: Coordinate Plane Race – Pair up and receive coordinates – Plot points on the coordinate plane – Calculate the distances between points – Use the distance formula or count squares – Compete to solve problems accurately – The pair with the most correct answers wins | This interactive class activity is designed to help students apply their knowledge of the coordinate plane and the concept of distance between two points. Students will work in pairs to foster collaboration. Each pair will receive a set of coordinates to plot on a graph and will then calculate the distance between those points. They can use the distance formula or count the squares on the graph paper if they are working with whole numbers. The competitive element aims to engage students and encourage accuracy. As a teacher, prepare several sets of coordinates in advance and ensure they vary in difficulty. Monitor the class to ensure that all students are participating and offer guidance as needed. Possible variations of the activity could include a relay race format, incorporating obstacles, or using real-world map coordinates for an added challenge.

Wrapping Up: Distance Between Points – Recap: Calculating distance – Accuracy & precision matter – Exact measurements are crucial in math and real-life applications. – Homework: 5 problem worksheet – Apply today’s lesson to solve problems on the worksheet. – Practice makes perfect | As we conclude today’s lesson on the distance between two points, remind students of the key formula and steps used to calculate the distance on a coordinate plane. Emphasize the importance of accuracy and precision in their calculations, as these skills are vital in various real-world contexts, such as engineering and navigation. For homework, students are assigned a worksheet with 5 problems to reinforce their understanding and application of the distance formula. Encourage them to practice diligently, as mastery comes with practice. The worksheet should be designed to cover a range of difficulties, ensuring that students can approach and solve each problem with confidence.