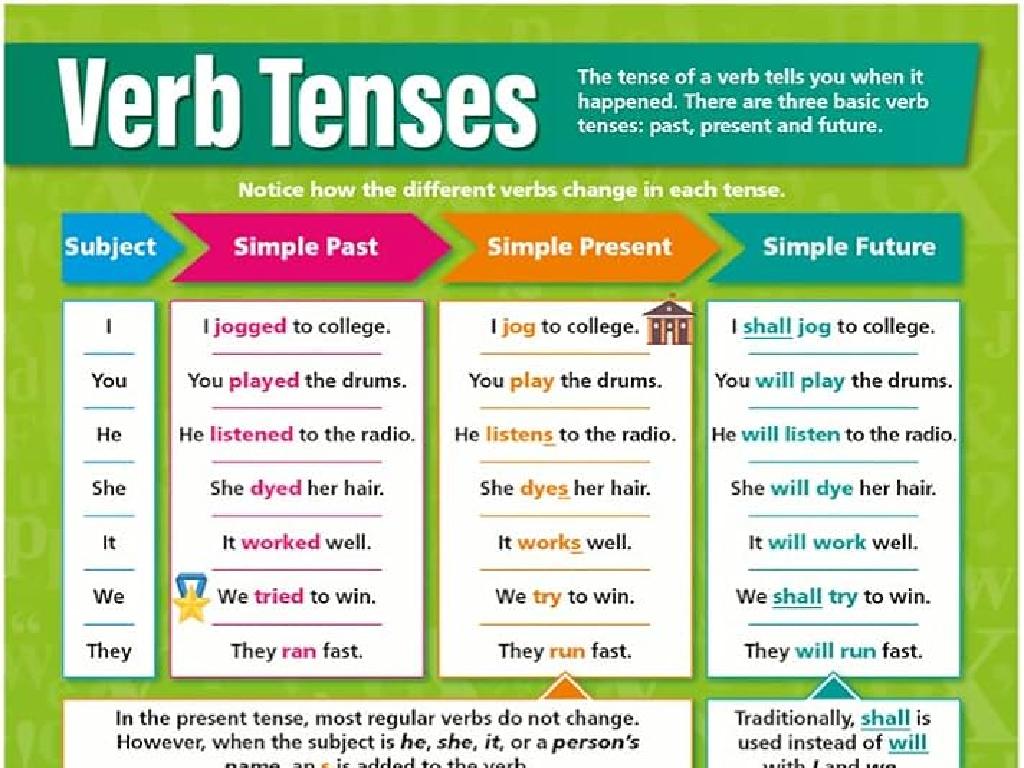
Quadrants And Axes
Subject: Math
Grade: Eighth grade
Topic: Coordinate Plane
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Exploring Quadrants and Axes
– Define coordinate plane
– A two-dimensional plane with a horizontal and vertical axis.
– Today’s focus: Quadrants & Axes
– Four quadrants created by x and y axes intersection.
– Real-life applications
– GPS navigation, video games, and graphing data.
– Understanding algebra foundations
– Coordinate planes are essential in algebra to visualize equations and inequalities.
|
Begin with a definition of the coordinate plane, emphasizing its importance as the foundation of algebra. Explain how the intersection of the horizontal (x-axis) and vertical (y-axis) axes divides the plane into four quadrants. Discuss real-life applications of coordinate planes, such as GPS navigation systems, video game graphics, and graphing data in various fields. Highlight how understanding quadrants and axes is crucial for students to visualize and solve algebraic equations and inequalities. Encourage students to think of additional examples where they encounter coordinate planes in their daily lives.
Exploring the Coordinate Plane
– Define the coordinate plane
– A two-dimensional plane for graphing points, lines, and curves using a pair of numbers.
– Significance of x-axis and y-axis
– The x-axis is horizontal, y-axis is vertical; they divide the plane into four quadrants.
– Origin: The coordinate plane’s start
– The point (0,0) where the x-axis and y-axis intersect; it’s the reference point for all other points.
– Understanding quadrants
– Quadrants are numbered I to IV, starting from the upper right and moving counter-clockwise.
|
The coordinate plane is a fundamental concept in mathematics that allows us to visually represent algebraic equations and geometric figures. The x-axis and y-axis are perpendicular lines that create a reference frame for locating points. The origin is the central point where these axes intersect and is the basis for determining the position of all other points on the plane. Understanding the layout of the quadrants is crucial for graphing and interpreting points and equations. Encourage students to remember the order and signs of the quadrants: Quadrant I (positive, positive), Quadrant II (negative, positive), Quadrant III (negative, negative), and Quadrant IV (positive, negative).
Meet the Axes: Dividing the Coordinate Plane
– X-axis: The horizontal line
– Y-axis: The vertical line
– Axes divide plane into quadrants
– The X and Y axes intersect at the origin (0,0)
– Quadrants are numbered I to IV
– Quadrants are labeled counterclockwise starting from the top right
|
This slide introduces students to the fundamental components of the coordinate plane: the X-axis and Y-axis. The X-axis runs horizontally and the Y-axis runs vertically, intersecting at the origin point (0,0). It’s crucial for students to understand that the intersection of these axes creates four distinct sections, known as quadrants, which are used to locate points in a two-dimensional space. The quadrants are numbered from I to IV, starting in the top right quadrant and moving counterclockwise. Emphasize the importance of the axes and quadrants in graphing and understanding the position of points in a coordinate system. Provide examples of points in different quadrants to illustrate their positions relative to the axes.
Exploring Quadrants on the Coordinate Plane
– Quadrant naming: I, II, III, IV
– Each quadrant’s characteristics
– Quadrant I: (+, +), II: (-, +), III: (-, -), IV: (+, -)
– Plotting example points
– (3, 2) in I, (-3, 4) in II, (-2, -5) in III, (4, -3) in IV
– Understanding axes intersections
– Axes intersect at the origin, dividing the plane into four quadrants
|
This slide introduces students to the concept of quadrants on the coordinate plane. Begin by explaining the naming convention for the quadrants, starting with Quadrant I in the top-right and moving counter-clockwise. Discuss the characteristics of each quadrant, noting the sign of the x and y coordinates in each. Provide example points for students to plot, reinforcing the concept of positive and negative values on the axes. Emphasize the importance of the origin (0,0) where the x-axis and y-axis intersect, creating the four distinct quadrants. Encourage students to practice by identifying the quadrant for given points and plotting their own examples.
Plotting Points on the Coordinate Plane
– Plotting a point with (x, y) coordinates
– To plot a point, locate the x value on the horizontal axis, then the y value on the vertical axis.
– Let’s practice plotting points
– We’ll plot points as a class to reinforce learning.
– Positive vs. negative values
– Values can be positive (above or right of the origin) or negative (below or left of the origin).
– Quadrants of the coordinate plane
– The plane is divided into four quadrants, each with a unique combination of positive and negative values.
|
This slide introduces students to the basics of plotting points on the coordinate plane. Start by explaining the coordinate system, where each point is defined by an x (horizontal) and y (vertical) value. Engage the class in an interactive plotting activity to solidify their understanding. Discuss how the signs of the x and y values determine the position of the point in relation to the origin (0,0). Emphasize the importance of recognizing positive and negative values, as this will help them identify which quadrant the point lies in. The four quadrants are crucial for understanding the layout of the coordinate plane and will be a foundation for future lessons in graphing equations and inequalities.
Quadrants in Real Life
– Navigating with map quadrants
– Maps are divided into quadrants for easier navigation.
– Video game character coordinates
– Characters move within a coordinate system, similar to quadrants.
– Graphing data in science
– Scientists plot data on graphs using the four quadrants.
– Understanding axes and quadrants
|
This slide aims to show students how the concept of quadrants and axes is applied in everyday life. When using maps, for example, understanding quadrants can help with navigation and location finding. In video games, players often use coordinates to navigate virtual worlds, which is a direct application of the coordinate plane. In science, particularly in fields like biology and physics, data is frequently plotted on graphs that use four quadrants, allowing for a clear visual representation of relationships and patterns. Encourage students to think of other areas where quadrants might be used and to consider the importance of the x and y-axes in organizing information.
Class Activity: Coordinate Plane Treasure Hunt
– Understand the game rules
– Use the coordinate plane for clues
– Each clue leads to a point on the plane
– Work in pairs to plot a course
– Collaborate to connect points and form a path
– Find the treasure using math
– Apply knowledge of quadrants and axes to locate the treasure
|
This activity is designed to reinforce students’ understanding of the coordinate plane, quadrants, and axes in a fun and interactive way. Students will work in pairs to solve clues that lead them to different points on a coordinate plane. Each clue will require them to plot a point, and the sequence of points will lead them to the ‘treasure’. Provide students with a map of the coordinate plane and a set of clues. Possible variations of the activity could include having different sets of clues for each pair, clues that require solving math problems to find the coordinates, or a timed challenge to add excitement. The goal is to help students apply their knowledge of the coordinate system in a practical and engaging context.
Conclusion & Homework: Quadrants and Axes Mastery
– Recap: Quadrants and Axes
– Mastery benefits future math
Understanding quadrants and axes is crucial for graphing functions and solving geometry problems.
– Homework: Plotting Points Worksheet
Complete the worksheet by plotting the given points on a coordinate plane.
– Identify quadrants for each point
Determine which quadrant each plotted point falls into.
|
As we conclude today’s lesson on quadrants and axes, it’s important to emphasize the role this foundational concept plays in higher-level mathematics, including algebra and geometry. Mastery of this topic will aid in graphing linear equations, understanding geometric shapes, and interpreting data in a coordinate plane. For homework, students are assigned a worksheet that requires them to plot a series of points on a coordinate plane and identify the quadrants where these points are located. This exercise will reinforce their understanding and help them practice the skills learned in class. Encourage students to review their notes and reach out if they have questions while completing the assignment.