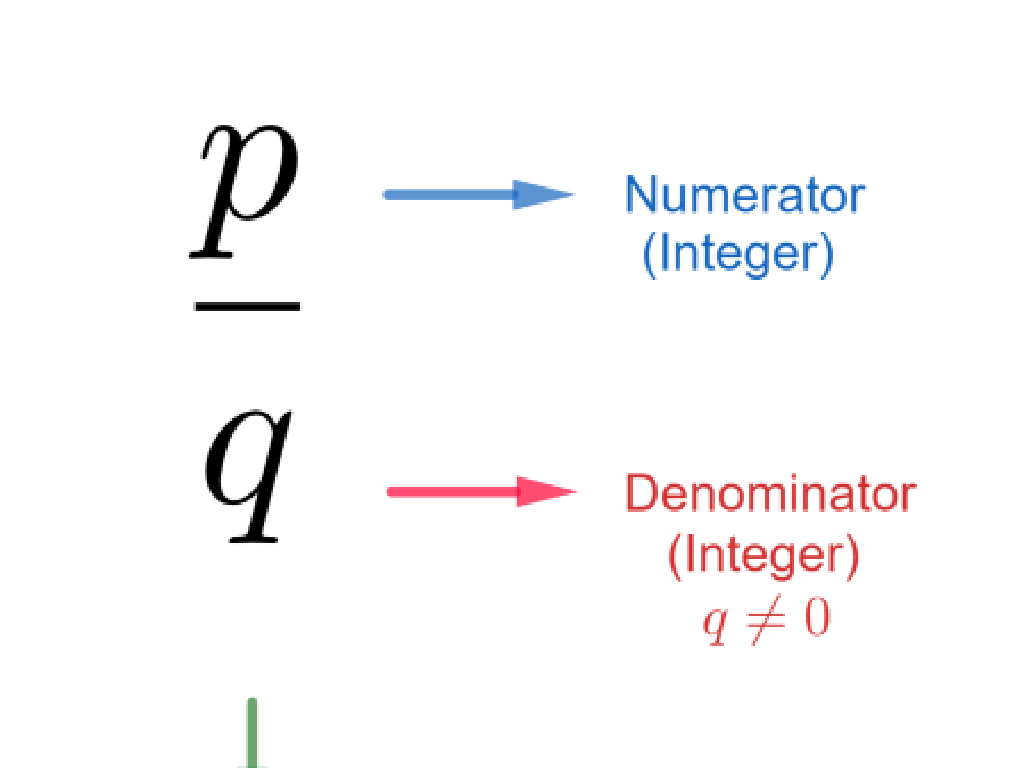
Divisibility Rules
Subject: Math
Grade: Sixth grade
Topic: Divide Whole Numbers
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Introduction to Divisibility
– What does ‘divisible’ mean?
– A number is divisible by another if it divides evenly with no remainder.
– Division in daily life
– Dividing pizza slices, sharing candies equally among friends.
– Overview of divisibility rules
– Rules that help us quickly determine if one number can be divided by another without actually doing the division.
– Why divisibility matters
– Understanding these rules simplifies math problems and helps in real-life situations like splitting bills.
|
This slide introduces the concept of divisibility, which is foundational for understanding division and its applications. Begin by explaining that a number is divisible by another if it can be divided evenly without leaving a remainder. Relate this to everyday scenarios, such as sharing items equally, to make the concept more tangible for students. Preview the rules for divisibility, which are shortcuts that help us determine divisibility without performing the full division. Emphasize the importance of these rules in making calculations easier and quicker, both in math problems and in practical situations like dividing goods or money. Encourage students to think of examples where they have used division in their lives.
Divisibility by 2
– Rule for divisibility by 2
– Ends in 0, 2, 4, 6, or 8? It’s divisible by 2.
– Examples of even numbers
– 14, 26, and 82 are all divisible by 2.
– Practice identifying divisibility
– Which of these are divisible by 2: 31, 44, 57, 68?
– Understanding even and odd
– Even numbers are divisible by 2, odd numbers are not.
|
This slide introduces the concept of divisibility, specifically focusing on the rule for divisibility by 2. It’s important to emphasize that any number ending in 0, 2, 4, 6, or 8 is divisible by 2, which also makes it an even number. Provide clear examples of even numbers to illustrate this point. For the practice activity, present a mix of numbers and ask students to identify which are divisible by 2, reinforcing their understanding of the rule. Additionally, explain the concept of even and odd numbers, as this is foundational for recognizing patterns in divisibility.
Divisibility by 3
– Rule for divisibility by 3
– If a number’s digits add up to a multiple of 3, it’s divisible by 3.
– Adding digits together
– For example, 123: 1 + 2 + 3 = 6, which is divisible by 3.
– Practice with example numbers
– Try 156 and 210 to see if they’re divisible by 3.
– Test your own numbers
– Choose any number and apply the rule to test divisibility.
|
This slide introduces the concept of divisibility by 3. The rule is straightforward and can be applied by adding up the digits of any number to see if the sum is divisible by 3. For instance, with the number 123, students add 1 + 2 + 3 to get 6, which is divisible by 3, so 123 is also divisible by 3. Provide practice numbers for the class to work through together, such as 156 (1 + 5 + 6 = 12, which is divisible by 3) and 210 (2 + 1 + 0 = 3, which is divisible by 3). Then, encourage students to test their own numbers to solidify their understanding. This activity helps students recognize patterns and apply mathematical rules to enhance their division skills.
Divisibility by 5
– Rule for divisibility by 5
– Ends in 0 or 5? It’s divisible by 5.
– Examples: Numbers divisible by 5
– 15, 30, 45, 60 all end in 5 or 0.
– Practice divisibility identification
– Is 22 divisible by 5? What about 35?
|
This slide introduces the concept of divisibility specifically focusing on the number 5. The rule is straightforward: if a number ends in 0 or 5, it is divisible by 5. Provide students with clear examples such as 15, 30, 45, and 60 to illustrate this rule. For the practice activity, present a list of numbers and ask students to determine which are divisible by 5, reinforcing their understanding of the rule. Encourage students to explain why a number is or isn’t divisible by 5 to develop their reasoning skills. This exercise will help solidify their grasp of divisibility rules, which are fundamental in number theory and essential for understanding fractions and factoring.
Divisibility by 10
– Rule for divisibility by 10
– A number ends in 0, it’s divisible by 10
– Place value system role
– The last digit’s place value is crucial
– Practice sorting numbers
– Sort a list of numbers into divisible / not divisible by 10
– Recognize patterns in divisibility
|
This slide introduces the concept of divisibility, specifically focusing on the rule for divisibility by 10. It’s important for students to understand that any number ending in 0 can be divided by 10 without a remainder, which is due to the place value system where the last digit represents the number of tens. To practice, students will sort a given set of numbers into two groups: those that are divisible by 10 and those that are not. This exercise will help them recognize the pattern and reinforce their understanding of the place value system. Encourage students to explain why a number is or isn’t divisible by 10 to deepen their comprehension.
Mastering Divisibility Rules
– Divisibility by 4: Last two digits
– If the last two digits of a number are divisible by 4, so is the whole number.
– Divisibility by 6: Even number and sum divisible by 3
– A number is divisible by 6 if it’s even and its digits add up to a multiple of 3.
– Divisibility by 8: Last three digits
– Check the number formed by the last three digits; if that’s divisible by 8, the whole number is too.
– Divisibility by 9 and 11: Special patterns
– For 9, if the sum of the digits is divisible by 9; for 11, if the alternating sum of digits is 0 or divisible by 11.
|
This slide introduces students to the divisibility rules for 4, 6, 8, 9, and 11. For 4, students should look at the last two digits of the number. If that two-digit number can be divided by 4, then the whole number can. For 6, the number must be even, and the sum of all digits should be divisible by 3. For 8, the last three digits are the focus, and if they form a number divisible by 8, the entire number is as well. For 9, the sum of all digits should be divisible by 9, and for 11, the alternating sum of digits (subtracting and adding each consecutive digit from left to right) should result in 0 or a number divisible by 11. The group activity will involve creating a chart that visually represents these rules, which will serve as a handy reference for students. Provide examples for each rule and encourage students to come up with their own examples during the activity. Prepare to facilitate the group activity by ensuring students understand the rules and can apply them to create their chart.
Class Activity: Divisibility Challenge
– Pair up for divisibility puzzles
– Solve and note your strategies
– Did you use known divisibility rules or patterns?
– Share findings with the class
– Reflect on divisibility strategies
– Discuss what worked and what didn’t
|
This activity is designed to encourage collaborative problem-solving and to reinforce the understanding of divisibility rules. Students will work in pairs to solve a series of puzzles that require them to apply divisibility rules for numbers 2, 3, 5, 9, and 10. After solving the puzzles, each pair will share their findings with the class, discussing the strategies they used. Encourage students to reflect on the effectiveness of their approaches, fostering a deeper understanding of how divisibility rules can be used to simplify math problems. Possible activities: 1) Finding numbers divisible by both 2 and 3 within a range, 2) Creating a list of numbers divisible by 5 and explaining the pattern, 3) Using divisibility rules to solve a riddle, 4) Determining if a large number is divisible by 9, 5) Checking divisibility by 10 and explaining why the rule works.
Divisibility Rules: Recap and Homework
– Recap today’s divisibility rules
– Review rules for 2, 3, 5, 9, and 10
– Applying rules to real-life
– Use in budgeting, event planning
– Homework: divisibility worksheet
– Practice with provided problems
|
As we conclude today’s lesson, remind students of the divisibility rules for 2, 3, 5, 9, and 10. Emphasize the practicality of these rules in everyday life, such as dividing items evenly among people, budgeting, or planning events. For homework, students are to complete the divisibility worksheet, which includes a variety of problems to reinforce their understanding of the rules. Encourage them to attempt all problems and bring any questions to the next class. This practice will help solidify their grasp of the concept and prepare them for more complex division tasks.