Your next great Lessn starts here.

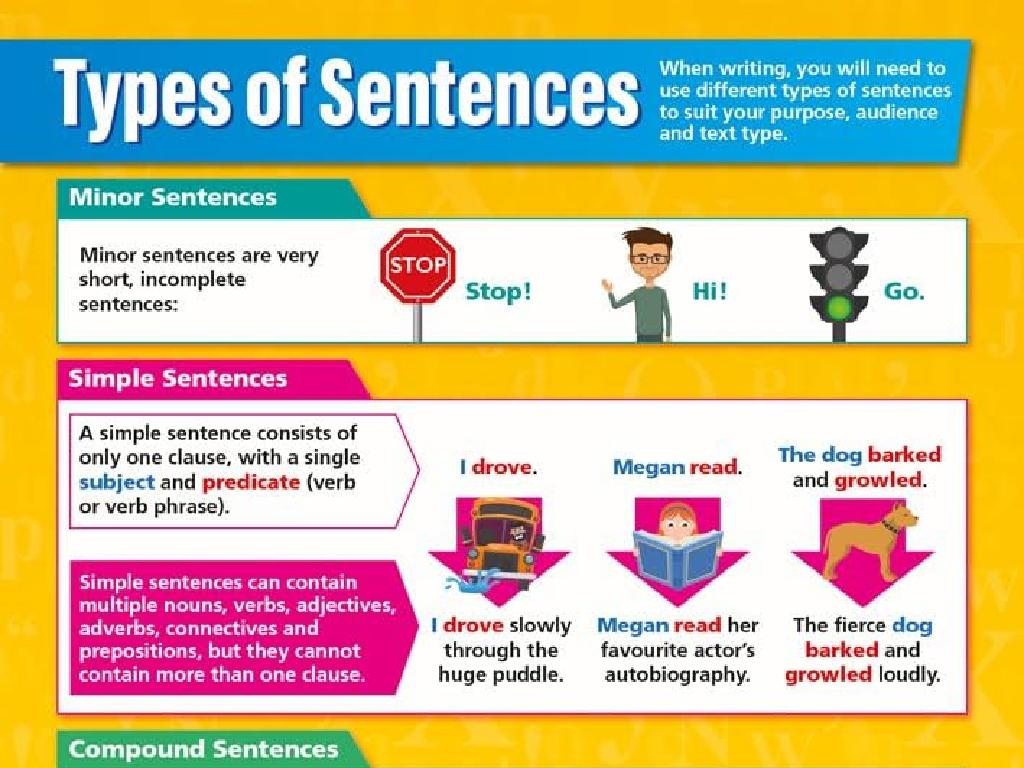
Properties of Addition and Multiplication – Explore Algebra’s language – Today’s focus: Addition & Multiplication – Commutative, Associative, Distributive properties – Importance of these properties – They form the foundation for solving equations – Practical applications – Use in simplifying expressions and solving real-world problems | This slide introduces students to the fundamental properties of addition and multiplication within the framework of algebra. It’s crucial to emphasize that understanding these properties is key to mastering algebraic expressions and equations. The commutative property (a+b=b+a or ab=ba), associative property ((a+b)+c=a+(b+c) or (ab)c=a(bc)), and distributive property (a(b+c)=ab+ac) allow us to rearrange and simplify expressions, which is essential for solving more complex problems. Highlight the relevance of these properties in everyday problem-solving and their role in various fields such as engineering, economics, and science. Encourage students to think of examples where they use these properties in daily life, like shopping or dividing tasks among friends.

Properties of Addition – Commutative Property – Order doesn’t affect sum: 3 + 5 = 5 + 3 – Associative Property – Grouping doesn’t change sum: (2 + 4) + 6 = 2 + (4 + 6) – Identity Property – Adding zero keeps identity: 7 + 0 = 7 – Real-life examples – Balancing a checkbook or combining items in a shopping cart | This slide introduces the fundamental properties of addition that are essential for understanding equivalent expressions. The commutative property indicates that the order of numbers does not affect the sum. The associative property shows that how numbers are grouped in addition does not change the result. The identity property states that adding zero to any number will not change its value. Provide real-life examples such as balancing a checkbook or combining items in a shopping cart to illustrate these properties in a way that is relatable to eighth-grade students. Encourage students to think of their own examples and to recognize these properties in everyday mathematical situations.

Properties of Multiplication – Commutative Property – Order doesn’t matter: 3 × 4 = 4 × 3 – Associative Property – Grouping doesn’t change product: (2 × 3) × 5 = 2 × (3 × 5) – Identity Property – Multiplying by one gives the same number: 7 × 1 = 7 – Distributive Property – Multiply inside the bracket first: 6 × (2 + 3) = 6 × 2 + 6 × 3 | This slide introduces the fundamental properties of multiplication that are essential for understanding equivalent expressions. The commutative property indicates that the order of multiplication does not affect the product. The associative property shows that the way numbers are grouped in multiplication does not change the product. The identity property states that any number multiplied by one remains unchanged. The distributive property allows us to multiply a number by a sum by multiplying each addend separately and then adding the products. Provide examples with both numbers and variables to illustrate each property. For instance, using variables, the distributive property can be shown as x(y + z) = xy + xz. Encourage students to apply these properties to simplify expressions and solve problems in algebra.

Applying Properties to Simplify Expressions – Combine like terms using properties – Simplify: 3x + 5x – Use Commutative: 5x + 3x = 8x, Associative: (3x + 5x) = 8x – Simplify: 2(a + 4) + 3(a + 4) – Distributive: 2a + 8 + 3a + 12 = 5a + 20 – Practice with different expressions | This slide aims to teach students how to simplify algebraic expressions using the properties of addition and multiplication. Start by explaining the concept of combining like terms and how properties like Commutative and Associative can be applied. For example, 3x + 5x can be simplified by rearranging and grouping like terms to get 8x. Next, demonstrate the Distributive Property by expanding 2(a + 4) + 3(a + 4) to get 5a + 20. Encourage students to practice these properties with various expressions to build their confidence in simplifying expressions. Provide additional examples and exercises for students to work on, ensuring they grasp the concept of using properties to simplify expressions effectively.

Practice Problems: Simplifying Expressions – Simplify: 6 + 2 + 4 – Use commutative property: 6 + 2 + 4 = 12 – Combine like terms: 7x + 3 + x + 2 – Group x terms and constants: 7x + x + 3 + 2 = 8x + 5 – Distribute and combine: 5(2 + 3x) + 4(3x + 2) – Apply distributive property, then combine like terms – Share your solutions | This slide is designed for a class activity where students will apply the properties of addition and multiplication to simplify algebraic expressions. Start with the commutative property of addition to rearrange and add numbers in Problem 1. For Problem 2, guide students to identify and combine like terms, which in this case are the terms with the variable x and the constant terms. In Problem 3, instruct students to use the distributive property to multiply the numbers outside the parentheses with each term inside the parentheses, then combine like terms. Encourage students to work through these problems individually or in small groups, and then share their solutions with the class. The teacher should circulate the room to offer assistance and ensure that students are correctly applying the properties. Possible variations for student activities include creating their own expressions to simplify or solving additional problems provided by the teacher.

Group Activity: Expression Creation – Form small groups of 3-4 – Create expressions with addition and multiplication – Combine numbers and variables creatively – Use properties to simplify expressions – Apply commutative, associative, distributive properties – Present simplified expressions to class | This group activity is designed to encourage collaboration and application of mathematical properties. Students should be divided into small groups to foster teamwork. They will create their own mathematical expressions using addition and multiplication, then apply the commutative, associative, and distributive properties to simplify these expressions. After simplification, each group will present their original and simplified expressions to the class, explaining the properties they used. This will help students understand the practical use of these properties in simplifying expressions. Possible activities: Group A simplifies using commutative property, Group B uses associative property, Group C applies distributive property, and Group D combines all properties.

Reflecting on Properties of Addition and Multiplication – Recap of today’s lesson – Application of properties in problem-solving – How commutative, associative properties simplify calculations – Share interesting insights – Maybe a certain property made an equation easier? – Discuss challenges faced – Was distributive property difficult to apply? | This slide aims to facilitate a class discussion reflecting on the day’s lesson about the properties of addition and multiplication. Encourage students to think about how the commutative, associative, and distributive properties can make solving equations more straightforward. Ask them to share any interesting observations they had during the lesson or any challenges they encountered. This will help reinforce their understanding and allow them to learn from each other’s experiences. Provide examples of how these properties are used in problem-solving to guide the discussion.

Homework: Simplifying Expressions – Practice using properties to simplify – Complete the 10-problem worksheet – Focus on distributive, associative, and commutative properties – Be ready to discuss solutions – Understand properties’ application – See how properties make complex expressions simpler | This homework assignment is designed to reinforce students’ understanding of the properties of addition and multiplication as they apply to simplifying algebraic expressions. The worksheet will provide practice problems that require the use of the distributive, associative, and commutative properties. Encourage students to attempt each problem and show their work for full credit. In the next class, we will review the worksheet answers and discuss any challenges faced. This will help students to clarify doubts and solidify their grasp of the concepts. Remind them that understanding these properties is crucial for working with equivalent expressions and will be beneficial in higher-level math.