Your next great Lessn starts here.

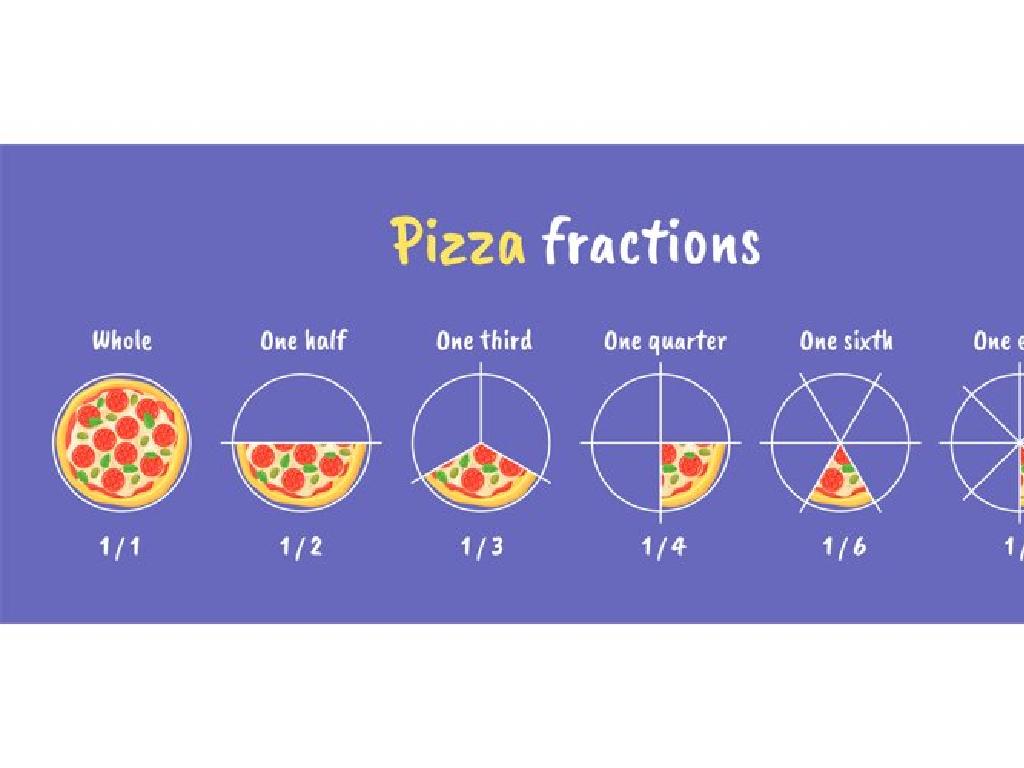
Exploring Equivalent Fractions with Area Models – What is a fraction? – A fraction represents a part of a whole. – Understanding equivalent fractions – Fractions that represent the same value. – Using area models to find equivalents – Visual method to compare fractions. – Today’s goal: Master equivalent fractions | Begin the lesson by explaining the basic concept of a fraction as a part of a whole, using examples like a slice of pizza or a piece of a chocolate bar. Then, introduce the concept of equivalent fractions, emphasizing that they are different fractions that represent the same amount. Use area models to visually demonstrate how to find equivalent fractions, showing that even though the number of pieces may differ, the overall size of the shaded area remains the same. The goal for today’s class is for students to understand and be able to find equivalent fractions using area models. Provide hands-on activities with different area models to reinforce the concept.

Understanding Fractions with Area Models – A fraction is part of a whole – Numerator and denominator explained – Top number (numerator) shows how many parts we have. Bottom number (denominator) shows into how many parts the whole is divided. – Example: 1/2 as a fraction – 1/2 means we have one part out of two equal parts of a whole. – Using area models for fractions – Draw a shape, divide it into equal parts, shade the parts to show the fraction. | Begin by explaining that a fraction represents a part of a whole, like a slice of pizza out of a whole pizza. Clarify the roles of the numerator and the denominator, using visual aids if possible. For example, show a circle (pizza) cut into two equal parts, with one part shaded to represent 1/2. Then, introduce area models as a visual way to understand fractions better. Area models can be shapes like rectangles or circles divided into equal parts, with some parts shaded to represent the fraction. This visual representation helps students grasp the concept of fractions more concretely.

Exploring Area Models for Fractions – Area models visualize fractions – Imagine a pizza cut into slices; each slice is a fraction of the whole pizza – Shapes divided into equal parts – If a square is cut into 4 equal parts, each part is 1/4 of the square – Shaded areas represent fractions – If 2 out of 4 parts are shaded, it shows 1/2 of the square is shaded – Comparing shaded parts – Look at two models to find equivalent fractions, like 1/2 and 2/4 | This slide introduces students to the concept of area models as a visual tool for understanding fractions. Area models help students see fractions as parts of a whole by dividing shapes into equal parts and shading some to represent a fraction. It’s crucial to emphasize that each part must be equal for the model to accurately represent the fraction. Encourage students to think of real-life examples, such as slices of pizza or pieces of a chocolate bar, to relate to the concept. In the next class, we’ll use area models to compare different fractions and find equivalents, reinforcing the idea that different-looking fractions can represent the same amount.

Understanding Equivalent Fractions – What are equivalent fractions? – Fractions that have the same value, even if they use different numbers. – Different looks, same value – Just like two different recipes can make the same cake! – Example: 1/2 equals 2/4 – Both fractions fill up the same amount of a shape when we draw them. – Using area models to compare – We’ll draw shapes and shade them to see how fractions can be the same. | This slide introduces the concept of equivalent fractions to third-grade students. Start by explaining that equivalent fractions are different fractions that represent the same part of a whole. Use relatable examples, such as different slices of the same size pizza, to illustrate this point. Show how 1/2 is the same as 2/4 by drawing two identical shapes and shading half of one and two-fourths of the other, demonstrating that the shaded areas are the same. This visual representation with area models will help students grasp the concept of equivalency in fractions. Encourage students to think of other examples and to use area models to verify if two fractions are equivalent.

Equivalent Fractions with Area Models – Draw two equal-sized models – Divide them into different parts – One model might have more parts, but both cover the same area – Shade equal areas in each – If half of each model is shaded, they show equivalent fractions – Compare shaded fractions | This slide introduces students to the concept of equivalent fractions using area models. Start by drawing two shapes of the same size, which will represent the same whole. Then, divide one shape into a certain number of parts (e.g., 4) and the other into a different number of parts (e.g., 8). Shade the same proportion of each model to illustrate that even though the number of parts is different, the shaded area represents the same fraction of the whole. For example, 1/2 can be shown as 2 out of 4 parts shaded or 4 out of 8 parts shaded. This visual representation helps students understand that fractions can look different but still be equivalent. Encourage students to create their own area models with different numbers of parts to find other equivalent fractions.

Let’s Practice Equivalent Fractions! – Draw area models on the board – Find fractions equivalent to 1/3 – For example, 2/6 is equivalent to 1/3 – Discuss equivalence with a partner – Share your thoughts and listen – Understand why they are equivalent – It’s because they occupy the same amount of space in a model | This slide is for a class activity focused on understanding equivalent fractions using area models. Start by drawing an area model for 1/3 on the board and then guide the students to draw their own. Next, work together to find other fractions that are equivalent to 1/3, such as 2/6 or 4/12, and draw area models for these as well. Encourage students to discuss with their partners why these fractions are equivalent, prompting them to notice that the models show the same area even though the number of parts is different. This activity will help solidify the concept of equivalent fractions and the use of area models to visualize them. Provide additional examples if needed and ensure that each student is engaged and understands the concept.

Your Turn: Exploring Equivalent Fractions – Complete the area model worksheet – Find and color equivalent fractions – Look for fractions that represent the same part of a whole – Share your findings in class – Discuss how you found equivalent fractions – Understand fractions through coloring – Coloring helps visualize how fractions are equal | This slide introduces an interactive class activity focused on understanding equivalent fractions through the use of area models. Students are tasked with completing a worksheet where they will find and color in areas representing equivalent fractions. This hands-on approach helps solidify the concept of equivalency by allowing students to see the fractions that occupy the same amount of space. Encourage students to use different colors for each set of equivalent fractions to enhance the visual learning experience. After completing the worksheet, students will be asked to share their findings with the class, promoting discussion and reinforcing their understanding. As a teacher, be prepared to guide students who may struggle with identifying equivalency and offer praise to those who demonstrate understanding.

Class Activity: Crafting Area Models – Draw area models using templates – Find two sets of equivalent fractions – Like 1/2 is same as 2/4, show it with models – Explain equivalence to a classmate – Use your models to show how the parts are equal – Discuss findings with the class | This activity is designed to help students understand the concept of equivalent fractions through a hands-on approach. Provide students with templates of area models, such as rectangles or circles divided into equal parts. Students will color in the parts to represent fractions and find at least two sets of equivalent fractions (e.g., 1/2 and 2/4, 1/3 and 2/6). They should then pair up with a classmate to explain why their fractions are equivalent, using their area models as visual aids. Afterward, facilitate a class discussion where students can present their models and explanations. This will reinforce their understanding and allow them to learn from each other. Possible variations of the activity could include using different shapes for the area models or challenging students to find more than two sets of equivalent fractions.

Conclusion: Understanding Equivalent Fractions – Recap equivalent fractions – Fractions with different numbers representing the same part of a whole – Area models clarify equivalence – Visual representations show how different shapes can represent the same fraction – Address lesson questions – Reinforce learning at home – Practice with more examples or use online fraction games | As we conclude today’s lesson, it’s important to review the concept of equivalent fractions to ensure understanding. Remind students that even though the numbers may be different, the fractions can represent the same amount. Area models are a great visual aid that helps students see this concept clearly. Take this time to answer any lingering questions students may have about equivalent fractions or the use of area models. Encourage them to continue practicing at home with additional worksheets or interactive online games that reinforce the concept of equivalent fractions.

Homework: Equivalent Fractions with Area Models – Practice equivalent fractions – Use area models on worksheet – Draw shapes divided into equal parts to represent fractions – Complete all worksheet problems – Discuss answers in next class – Think about how different shapes can show the same fraction | This homework assignment is designed to reinforce the concept of equivalent fractions using area models, which are visual representations that help students understand fractions better. The worksheet provided will have various shapes divided into parts, and students will color in parts to create equivalent fractions. Encourage students to try different area models and to be prepared to explain how they found their answers. In the next class, we will have a discussion to share different methods and to clarify any misunderstandings. This will help students to see the practical application of equivalent fractions and to learn from each other.