Your next great Lessn starts here.

Mastering Exponents: Finding the Missing Piece – Grasping exponent fundamentals – Exponents show how many times to use a number in a multiplication. – Recap: Exponents explained – An exponent has a base (number) and a power (exponent). – Today’s goal: Missing exponent/base – Use inverse operations to find the missing number in an equation like 2^x = 8. – Strategies to solve for unknowns – Apply division or logarithms to uncover the missing exponent, and roots for the base. | This slide introduces the concept of exponents and sets the learning objective for the class, which is to find the missing exponent or base in an exponential expression. Begin by reviewing the definition of exponents, emphasizing the base and the power. Explain that today’s lesson will focus on solving problems where either the base or the exponent is unknown. Provide strategies such as using inverse operations, such as logarithms for finding exponents and roots for finding the base. Ensure to give examples and practice problems to reinforce the learning objective. Encourage students to ask questions and work through problems together.

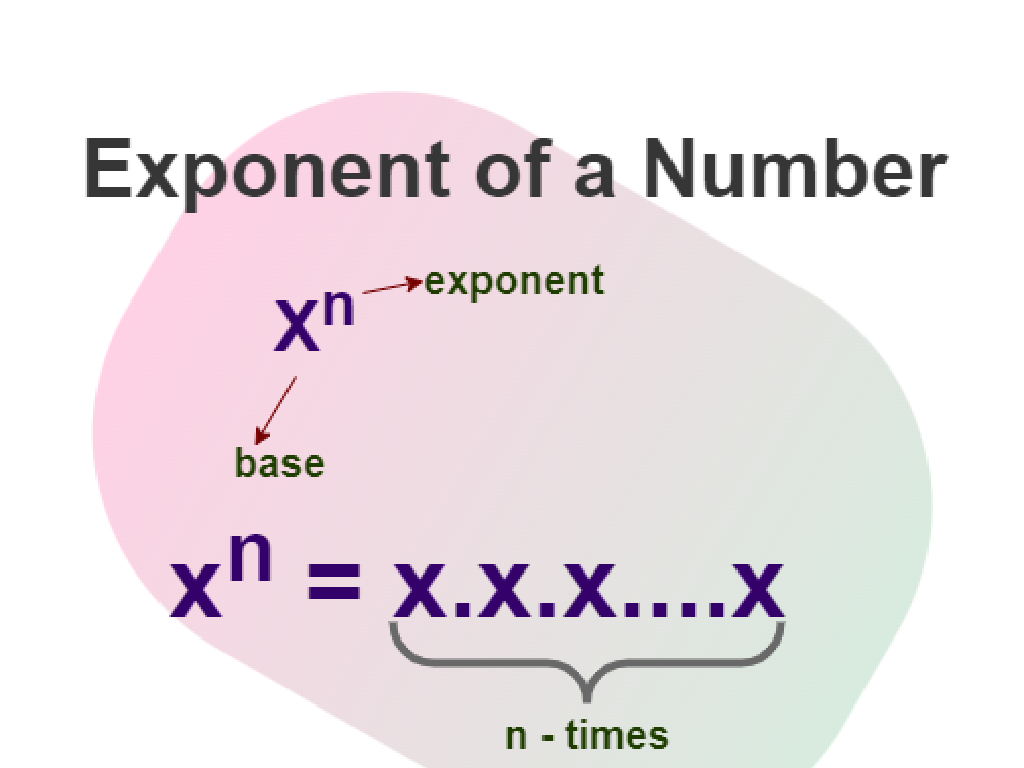
Understanding Exponents – Define an exponent – An exponent shows how many times a number, the base, is multiplied by itself. – Exponential expression parts – Base: the number being multiplied; Exponent: the number of times it’s multiplied. – Examples of exponential expressions – For 2^3, 2 is the base, 3 is the exponent, meaning 2 x 2 x 2. | This slide introduces the concept of exponents to the students. Begin with the definition of an exponent, emphasizing that it represents repeated multiplication, not just a number next to another. Clarify the parts of an exponential expression, pointing out the base and the exponent, and how each part plays a role in the expression’s value. Provide clear examples, such as 2^3 or 5^2, and demonstrate how to expand them into repeated multiplication. This foundational understanding will be crucial for learning how to find missing exponents or bases in future lessons.

Multiplication & Exponents: Simplifying Repetition – Exponents represent repeated multiplication – Example: 3^4 means 3 x 3 x 3 x 3 – 3 raised to the power of 4 is 3 multiplied by itself 4 times – Practice: Express 2^5 in long form – Write 2 multiplied by itself 5 times – Understanding the base and exponent – The base is the number being multiplied; the exponent tells how many times | This slide introduces the concept of exponents as a way to simplify repeated multiplication. Start by explaining that an exponent tells us how many times to multiply a number (the base) by itself. Use 3^4 as an example to show that it’s the same as multiplying 3 by itself four times. Then, have the students practice by writing out 2^5 as repeated multiplication. This exercise helps them understand the relationship between the base and the exponent. Encourage students to think of exponents as a shortcut for writing out multiplication and to recognize patterns in exponential expressions.

Finding the Missing Exponent – Steps to solve for missing exponent – Identify the base and the result. Use logarithms or patterns to find the exponent. – Example: 2 raised to what equals 8? – 2^3 = 8, so the missing exponent is 3. – Practice Problem: 5 to the power of ? equals 125 – 5^3 = 125, thus the missing exponent is 3. | This slide introduces the concept of finding a missing exponent in an equation. Start by explaining the components of an exponential expression, where the base is raised to an exponent to get a result. To find a missing exponent, students can look for patterns or use logarithms. For example, since 2 multiplied by itself three times equals 8, the missing exponent when 2 is raised to what equals 8 is 3. Similarly, for the practice problem, since 5 multiplied by itself three times equals 125, the missing exponent is 3. Encourage students to solve these problems by recognizing patterns of exponents with familiar bases. Provide additional practice problems with different bases to solidify their understanding.

Finding the Missing Base in Exponents – Steps to solve for missing base – Identify the exponent, rewrite the equation as a root – Example: ?^3 = 27 – Cube root of 27 is 3, so 3^3 = 27 – Practice Problem: ?^2 = 49 – Square root of 49 is 7, so 7^2 = 49 | This slide is focused on teaching students how to find a missing base when dealing with exponents. Start by explaining the steps to solve for the missing base, which includes identifying the exponent and rewriting the equation as a root problem. Use the example to show how to find the cube root of 27, which is 3, to determine that the missing base is 3. Then, present the practice problem and guide students to find the square root of 49, which is 7, indicating that the missing base for the equation ?^2 = 49 is 7. Encourage students to solve similar problems and understand the relationship between roots and exponents. Provide additional practice problems for students to work on individually or in groups.

Using Logs to Find the Missing Piece – Introduction to logarithms – Logarithms are the inverse of exponentiation. – Logs reveal missing exponents – If b^x = y, then log_b(y) = x helps find x. – Example: log2(8) = ? – log2(8) asks for what power of 2 gives 8? Answer: 3 – Practice with different bases – Try finding log10(100), log3(9), and log5(25) | This slide introduces the concept of logarithms to students as a method for finding missing exponents in equations. Begin by explaining that logarithms are the opposite of exponents and can be used to solve for an unknown exponent. Use the example log2(8) to illustrate how to find the power that 2 must be raised to in order to get 8, which is 3. Encourage students to practice with different bases to solidify their understanding. Provide guidance on how to read logarithmic expressions and how to translate them into their exponential form for easier comprehension.

Class Activity: Exponent Detective – Solve Mystery Exponents – Pair up for detective work – Find missing bases and exponents – Present your findings | In this engaging class activity, students will work in pairs to solve ‘mystery exponents’. Each pair will receive a set of problems where they must deduce the missing base or exponent to complete the equation. For example, if given 3^x = 9, students must determine that x equals 2. After solving their set of problems, students will share their solutions with the class, explaining their reasoning and how they worked together to find the answers. This activity promotes collaboration, critical thinking, and a deeper understanding of how exponents function. Possible variations for different pairs could include finding the missing base instead of the exponent, or vice versa, and using different levels of difficulty for the problems.

Exponents: Review & Wrap-Up – Recap key exponent concepts We revisited base, exponent, and calculating power. – Significance of exponents Exponents are crucial for compactly writing large numbers and in various areas of math and science. – Homework: Solve exponent problems A set of problems to reinforce today’s lesson. – Be prepared to discuss solutions | As we conclude today’s lesson on exponents, it’s important to review the key concepts, including the base, exponent, and how to calculate the power of a number. Emphasize the importance of understanding exponents as they are widely used in higher-level math, science, and in understanding exponential growth in real-life scenarios. Assign a set of practice problems for homework to ensure students apply what they’ve learned. In the next class, be ready to discuss the solutions and clarify any doubts. This will help solidify their grasp of the topic and prepare them for more complex applications.