Your next great Lessn starts here.

Converting Improper Fractions and Mixed Numbers – What are improper fractions? Fractions where the numerator is greater than the denominator, e.g., 7/4. – What are mixed numbers? A combination of a whole number and a fraction, e.g., 1 3/4. – How to convert between them Divide the numerator by the denominator, the quotient is the whole number, the remainder is the new numerator. – Significance in math and life | This slide introduces students to the concept of improper fractions and mixed numbers, which are fundamental in understanding fractions and decimals. Improper fractions have numerators larger than their denominators, while mixed numbers combine whole numbers with fractions. Converting between these forms is a key skill in math that has practical applications in real life, such as measuring ingredients in cooking or dividing groups into smaller parts. Ensure students grasp the conversion process by providing examples and practice problems. Highlight the relevance of these concepts in everyday situations to help students appreciate their importance.

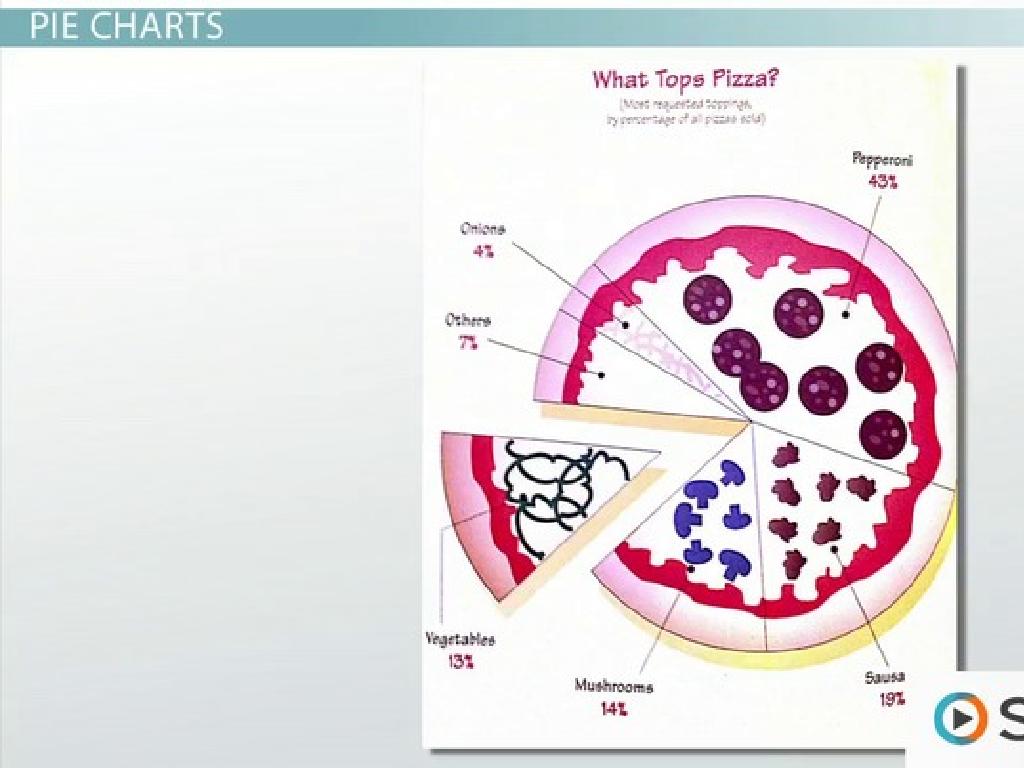
Understanding Fractions: Types and Visualization – Review: Numerator & Denominator – Top number is numerator, bottom is denominator – Types: Proper, Improper, Mixed – Proper fractions are less than 1, improper are more than 1, mixed numbers are a combination – Visualize with Pie Charts – Pie charts show fractions as parts of a whole – Use Number Lines – Number lines help place fractions in order | Begin with a quick review of the basic components of a fraction: the numerator and the denominator. Explain the difference between proper fractions (values less than 1), improper fractions (values greater than 1), and mixed numbers (a whole number and a fraction combined). Use pie charts to help students visualize fractions as parts of a whole, which can be particularly helpful for understanding improper fractions and mixed numbers. Introduce number lines as another tool for visualizing and comparing the size of fractions. This will set a strong foundation for learning how to convert between improper fractions and mixed numbers.

Understanding Improper Fractions – Define improper fraction – Numerator larger than or equal to denominator, e.g., 7/4 or 9/9 – Examples of improper fractions – 7/4, 9/8, 11/3 are all improper fractions – Identifying improper fractions – If the top number is bigger, it’s improper – Converting to mixed numbers | Begin by defining an improper fraction as a fraction where the numerator (top number) is larger than or equal to the denominator (bottom number). Provide examples of improper fractions to illustrate this concept. Explain that if students see the top number is bigger than the bottom number, they’re looking at an improper fraction. Then, demonstrate how to convert an improper fraction to a mixed number by dividing the numerator by the denominator to find the whole number, and then writing the remainder over the original denominator. This slide will help students recognize and convert improper fractions, a key skill in understanding fractions and decimals.

Understanding Mixed Numbers – Define a mixed number – A number with a whole part and a fraction part, e.g., 2 1/2 – Examples of mixed numbers – 3 3/4 (three and three-fourths), 5 1/2 (five and a half) – Identifying mixed numbers – Look for a whole number alongside a fraction – Practice with mixed numbers – Convert 7/2 and 11/4 to mixed numbers | A mixed number is composed of a whole number and a fraction, representing a value greater than or equal to 1. It’s important for students to recognize the two parts of a mixed number: the whole number and the fraction. Provide clear examples, such as 3 3/4, where 3 is the whole number and 3/4 is the fraction. Teach students to identify mixed numbers by looking for the presence of both a whole number and a fraction. To ensure understanding, have students practice converting improper fractions like 7/2 and 11/4 into mixed numbers, reinforcing the concept that the numerator can be greater than or equal to the denominator in improper fractions.

Converting Improper Fractions to Mixed Numbers – Use division: Numerator ÷ Denominator – Example: Convert 7/4 to 1 3/4 – 7 divided by 4 equals 1 with a remainder of 3. So, 7/4 = 1 3/4. – Practice: Convert 9/5 to a mixed number – Apply the division method to 9/5 and find the mixed number. – Understand mixed numbers – Mixed numbers have a whole part and a fraction part. | This slide introduces the concept of converting improper fractions to mixed numbers using the division method. Start by explaining that the numerator (top number) is divided by the denominator (bottom number) to find the whole number part of the mixed number. The remainder becomes the numerator of the fraction part. Use 7/4 as an example to show this process step by step. Then, provide a practice problem, 9/5, for students to try on their own. Emphasize the understanding of mixed numbers as numbers with both a whole part and a fraction part. Encourage students to work through the example and practice problem, and be ready to discuss their approach during the next class.

Converting Mixed Numbers to Improper Fractions – Understand Multiplication-Addition Method – Example: Convert 2 1/3 to an improper fraction – Multiply the whole number (2) by the denominator (3), then add the numerator (1). Result: 7/3 – Practice Problem: Convert 3 2/5 – Apply the method: 3*5 + 2 to find the improper fraction – Steps to convert mixed numbers – Multiply whole number by denominator, add numerator | This slide introduces the method for converting mixed numbers to improper fractions, which is a key skill in understanding fractions. Start by explaining the Multiplication-Addition Method: multiply the whole number by the denominator and add the numerator. Use the example of 2 1/3 to show this process step by step, resulting in 7/3. Then, present the practice problem of 3 2/5 and guide students through the conversion. Encourage students to work through the problem and understand each step. The goal is for students to become comfortable with this method and to apply it to various mixed numbers. Provide additional practice problems for students to work on independently, ensuring they grasp the concept.

Let’s Practice Together: Conversion Exercises – Convert 11/3 to a mixed number – Divide 11 by 3. The quotient is the whole number, and the remainder over 3 is the fraction. – Convert 4 3/8 to an improper fraction – Multiply the whole number 4 by the denominator 8, add 3, and place over 8. – Discuss steps with a partner – Explain your process and compare answers. – Share your results with the class | This slide is for a class activity where students will practice converting between improper fractions and mixed numbers. For the first exercise, guide students to divide the numerator by the denominator to find the whole number and the remainder, which becomes the fraction part of the mixed number. For the second exercise, instruct students to convert the mixed number to an improper fraction by multiplying the whole number by the denominator and adding the numerator. Encourage students to work in pairs to discuss their methods and results, fostering collaborative learning. After the activity, ask some pairs to share their results and discuss any differences in their approaches. This will help students understand different methods and reinforce their learning.

Real-World Applications of Fractions – Fractions in cooking and baking – Use 3/4 cup of sugar or 1 1/2 teaspoons of salt. – Measuring distances and lengths – A board might be 5/2 feet long, or 2 1/2 feet. – Understanding portions and servings – A pizza slice might be 1/8 of a pizza, or a mixed number if cut unevenly. – Converting for clarity and ease | This slide aims to show students how fractions are used in everyday life, making the concept more relatable and easier to understand. When cooking or baking, recipes often call for fractions of a cup or teaspoon. In construction or crafts, materials are often measured using fractions of standard units. Understanding portions, like how many slices make up a whole pizza, is another practical application. Encourage students to think of other examples where they encounter fractions and mixed numbers in their daily lives. This will help them grasp the importance of being able to convert between the two for clarity and ease in practical situations.

Class Activity: Fraction Scavenger Hunt – Find mixed numbers in the classroom – Locate improper fractions around – Convert each example found Change mixed numbers to improper fractions and vice versa – Share findings with the class | This interactive activity is designed to help students apply their knowledge of converting between mixed numbers and improper fractions in a fun and engaging way. Scatter various examples of mixed numbers and improper fractions around the classroom before the activity begins. Students will search for these examples and work on converting them to the other form. Encourage them to check their work with a partner before sharing with the class. This will not only reinforce their understanding but also promote collaboration. Possible variations of the activity could include a timed challenge, team competition, or creating their own examples for peers to find and convert.

Converting Fractions: Summary & Homework – Recap: Improper fractions to mixed numbers – Remember, divide the numerator by the denominator – Recap: Mixed numbers to improper fractions – Multiply the whole number by the denominator, then add the numerator – Mastery of conversions is crucial – Helps in simplifying expressions and solving problems – Homework: Practice worksheet | This slide aims to summarize the lesson on converting between improper fractions and mixed numbers. Emphasize the importance of understanding both conversion processes as they are fundamental skills in algebra and beyond. For homework, students are assigned a worksheet with 10 problems to reinforce their learning. This practice will help solidify their understanding and prepare them for more complex mathematical concepts. Encourage students to attempt the worksheet independently, and remind them to show their work for each problem to track their thought process.