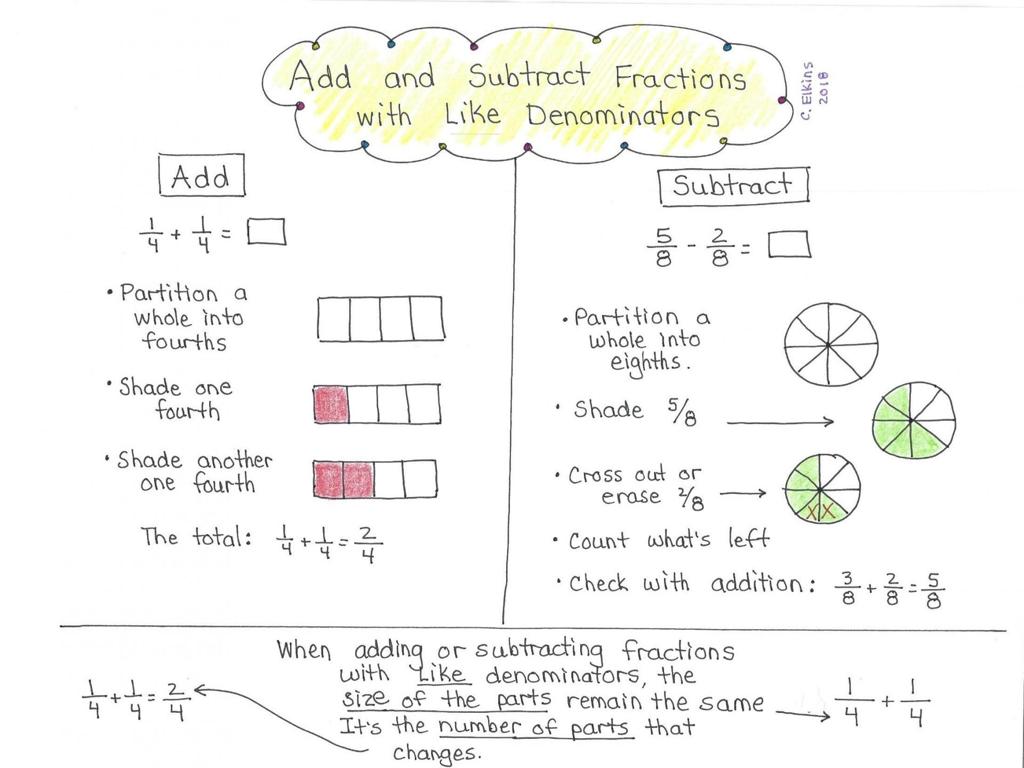
Convert Between Fractions And Repeating Decimals
Subject: Math
Grade: Sixth grade
Topic: Fractions And Decimals
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Converting Fractions and Repeating Decimals
– Understanding fractions and decimals
– Fractions represent parts of a whole; decimals represent the same using place value.
– Similarities and differences
– Both represent numbers between whole numbers; decimals use a point, fractions use a numerator/denominator.
– Converting fractions to decimals
– Divide the numerator by the denominator to convert to a decimal.
– Converting decimals to fractions
– Write the decimal as a fraction with a denominator of 9 for each repeating digit, then simplify.
|
This slide introduces the concept of converting between fractions and repeating decimals, a key skill in understanding the relationship between these two forms of numbers. Begin by discussing what fractions and decimals represent and how they are used to express values less than one whole. Highlight the differences in representation but emphasize their equivalence in value. Demonstrate the conversion process from fractions to decimals by division, and from decimals to fractions by using the place value system and simplification. Provide examples such as converting 1/3 to a decimal and 0.333… to a fraction. Encourage students to practice with different fractions and repeating decimals to gain confidence in this skill.
Understanding Fractions
– Definition of a fraction
– A fraction represents a part of a whole
– Numerator and denominator
– Top part is numerator, bottom part is denominator
– Fractions in daily life
– Pizza slices, measuring cups, and money (quarters)
– Converting fractions
|
Begin the lesson by defining a fraction as a part of a whole, which is divided into equal parts. Explain that the numerator (top number) indicates how many parts we have, while the denominator (bottom number) shows the total number of equal parts the whole is divided into. Provide relatable examples such as slices of pizza to represent fractions, or using measuring cups in cooking, and even money, where a quarter represents a fraction of a dollar. Emphasize that understanding fractions is essential for learning how to convert them into repeating decimals, which will be covered in subsequent slides. Encourage students to think of other examples of fractions they encounter in their daily lives.
Understanding Decimals
– Define a decimal
– A number with a whole part and a fractional part separated by a decimal point.
– Learn decimal places
– Each place after the decimal represents a fraction of a base 10.
– Decimals in daily life
– Money uses decimals: $1.25 means 1 dollar and 25 cents.
– Practice with examples
– Convert fractions like 1/2 to decimals by division: 1 ÷ 2 = 0.5.
|
This slide introduces students to the concept of decimals, which are an essential part of mathematics, especially when dealing with fractions and measurements. Start by defining a decimal and explaining the parts of a decimal number. Emphasize the importance of decimal places and how each place value represents tenths, hundredths, thousandths, etc. Use everyday examples, such as money, to illustrate how decimals are used in real life. Finally, engage students with simple conversion exercises from fractions to decimals to reinforce their understanding. Encourage students to bring examples of decimals they find at home or in stores to the next class for discussion.
Understanding Repeating Decimals
– Define repeating decimals
– Decimals where one or more digits repeat infinitely
– Notation for repeating decimals
– Use a bar over the repeating digits, e.g., 0.333… is 0.
– Examples of repeating decimals
– 1/3 as 0. 3, 1/6 as 0.1 6
|
This slide introduces students to the concept of repeating decimals, which are decimals that have a pattern of one or several numbers repeating endlessly. Emphasize the notation with a bar (vinculum) over the digits that repeat to signify the pattern continues indefinitely. Provide clear examples, such as converting common fractions to their repeating decimal form. For instance, 1/3 equals 0.333…, and we denote it as 0. 3 to show the 3 repeats forever. Similarly, 1/6 is 0.1666…, which we write as 0.1 6. Encourage students to practice with different fractions to become comfortable with the concept and notation of repeating decimals.
Converting Fractions to Repeating Decimals
– Divide numerator by denominator
– Spot the repeating decimal pattern
– Look for numbers that repeat in a cycle
– Notate the repeating decimal
– Use a bar over the repeating digits
– Practice with examples
– Try 1/3 = 0.333… or 2/9 = 0.222…
|
This slide introduces the process of converting fractions to repeating decimals, a key concept in understanding the relationship between fractions and decimals. Start by dividing the numerator (top number) by the denominator (bottom number) using long division. Then, identify the pattern of digits that repeats indefinitely. This pattern can be a single digit or a group of digits. Once the pattern is recognized, write the decimal with a bar over the repeating part to indicate it goes on forever. For example, 1/3 becomes 0.333…, and we write it as 0. 3 to show the 3 repeats. Encourage students to practice with different fractions to become comfortable with the process. Provide several examples and work through them as a class, ensuring to demonstrate how to write the repeating decimal notation correctly.
Converting Repeating Decimals to Fractions
– Set decimal equal to variable x
– If 0.333… is x, what equation can we write?
– Use algebra to remove repeats
– Multiply x by 10 or 100 to isolate the repeating part
– Solve for x to find the fraction
– After simplifying, x equals a fraction that represents the decimal
|
This slide introduces the process of converting repeating decimals to fractions, a key concept in understanding the relationship between these two numerical representations. Start by assigning the repeating decimal to a variable, typically x. This creates an equation that can be manipulated algebraically. To eliminate the repeating pattern, multiply the equation by a power of 10 that matches the length of the repeat. Subtract the original equation from this new equation to isolate x on one side, and solve for x, which will now be in fraction form. For example, to convert 0.333… to a fraction, set x = 0.333…, then 10x = 3.333…, subtract the original equation from this to get 9x = 3, and solve for x = 3/9, which simplifies to 1/3. Encourage students to practice this method with different repeating decimals to become comfortable with the process.
Converting Fractions and Repeating Decimals
– Convert 1/3 to a decimal
– 1/3 equals 0.333…
– Change 0.666… to a fraction
– 0.666… equals 2/3
– Classwork: 5/6 as a decimal
– Write 5/6 in decimal form
|
This slide is focused on practicing the conversion between fractions and repeating decimals. Start by demonstrating how to convert 1/3 into a repeating decimal by dividing the numerator by the denominator. Then, show the reverse process by converting the repeating decimal 0.666… into a fraction, which involves understanding that the repeating six represents an infinite series that can be summed up as 2/3. For classwork, guide students to convert 5/6 into a repeating decimal, reinforcing the method of long division. Encourage students to recognize patterns in repeating decimals and how they relate to their fraction counterparts. Provide additional examples if time permits, and ensure to clarify any doubts students may have during the process.
Class Activity: Fraction-Decimal Conversion Relay
– Split into teams for a relay
– Solve a conversion problem on board
– Convert fractions to repeating decimals and vice versa
– First team with correct answer advances
– Continue until one team wins
|
This activity is designed to encourage teamwork and reinforce the concept of converting between fractions and repeating decimals. Divide the class into small groups, ensuring a mix of abilities in each team. Provide each team with a different conversion problem to solve at the board. The first team to present a correct solution moves on to the next round, where they face a new problem. This continues until one team is declared the winner. Possible conversion problems include converting 1/3 to a decimal and converting 0.666… to a fraction. The teacher should prepare a list of conversion problems beforehand and ensure they are appropriate for the sixth-grade level. The teacher should also be ready to assist and provide hints if necessary.
Wrapping Up: Fractions & Decimals
– Review of fraction-decimal conversions
– We learned how to convert fractions to repeating decimals and vice versa.
– Why conversion mastery matters
– Conversions are key in math and real-life applications.
– Homework: 10 problem worksheet
– Practice with a worksheet to reinforce today’s lesson.
|
As we conclude today’s lesson on converting between fractions and repeating decimals, it’s crucial to emphasize the importance of mastering these conversions for future math concepts and everyday situations, such as understanding interest rates or measurement conversions. The homework assignment is a worksheet that includes 10 problems, designed to reinforce the methods taught in class. Encourage students to attempt each problem and remind them that practice is essential for mastery. During the next class, we will review the homework answers and clarify any misunderstandings.