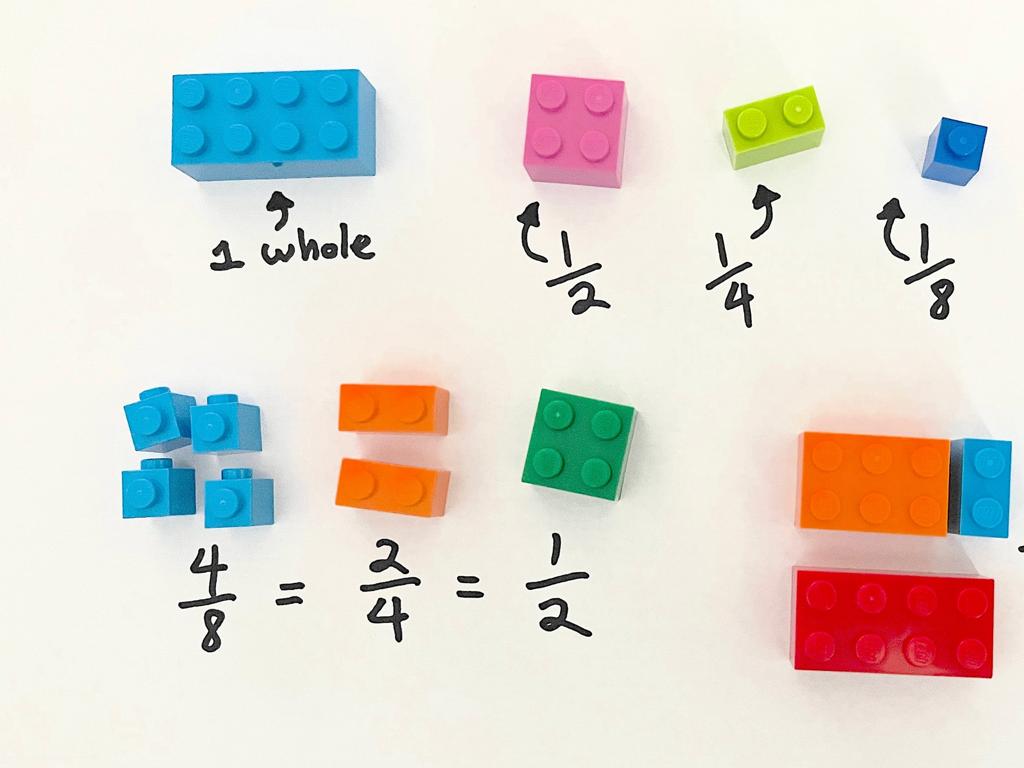Your next great Lessn starts here.

Writing Fractions in Lowest Terms – Recap: What are fractions? – Fractions represent parts of a whole. – Simplifying fractions: Why? – Simplified fractions are easier to compare and work with. – Steps to write in lowest terms – Find the greatest common divisor (GCD) and divide the numerator and denominator by it. – Practice simplifying fractions – Let’s try simplifying 4/8 or 10/25 together. | Begin with a brief review of what fractions are, ensuring students recall that fractions represent parts of a whole. Emphasize the importance of simplifying fractions, explaining that it makes them easier to read, compare, and use in calculations. Walk through the steps of finding the greatest common divisor (GCD) of the numerator and denominator and then dividing both by the GCD to simplify the fraction. Provide several examples for the class to work through together, such as simplifying 4/8 to 1/2 or 10/25 to 2/5, reinforcing the concept. Encourage students to ask questions and offer their own examples to ensure understanding.

Understanding Fractions in Lowest Terms – Lowest terms: simplest form – A fraction is in lowest terms when numerator and denominator have no common factors other than 1. – Examples: Simplified fractions – 1/2 is already in lowest terms, but 4/8 can be simplified to 1/2. – Find the GCD for lowest terms – GCD is the largest number that divides both numerator and denominator without a remainder. – Use GCD to simplify fractions – Divide both top and bottom by the GCD to write the fraction in lowest terms. | This slide introduces the concept of fractions in their lowest terms, which is a fundamental skill in understanding and simplifying fractions. Begin by explaining that a fraction is in its lowest terms when it cannot be made any simpler without changing its value. This means the numerator and denominator have no common factors except for 1. Provide clear examples of fractions that are already in lowest terms and those that can be simplified. Emphasize the importance of finding the Greatest Common Divisor (GCD) of the numerator and denominator as a step to simplifying fractions. Demonstrate how to use the GCD to reduce fractions to their simplest form. Encourage students to practice this skill with various examples.

Finding the Greatest Common Divisor (GCD) – Define the Greatest Common Divisor – GCD is the largest number that divides two numbers without a remainder. – List factors to find the GCD – Write down all factors of two numbers and find the largest common one. – Explore the Euclidean Algorithm – A method to find GCD for big numbers by dividing and taking remainders. – Simplify fractions using GCD – Use the GCD to reduce fractions to their simplest form. | This slide introduces the concept of the Greatest Common Divisor (GCD), an essential part of simplifying fractions. Start by defining GCD and explaining its role in reducing fractions to their lowest terms. Demonstrate the listing method by finding factors of smaller numbers and identifying the largest common factor. For larger numbers, introduce the Euclidean Algorithm as a systematic way to find the GCD. Emphasize the importance of the GCD in simplifying fractions, and provide examples to practice. Encourage students to work through problems step-by-step and verify their answers.

Simplifying Fractions Step by Step – Divide by the Greatest Common Divisor (GCD) – Find GCD of numerator & denominator, then divide both by it – Check if the fraction is fully simplified – A fraction is fully simplified when no number except 1 can divide both – Practice with different fractions – Example: Simplify 8/12. GCD is 4, so 8÷4/12÷4 = 2/3 | This slide introduces the process of simplifying fractions, a fundamental skill in understanding fractions. Start by explaining the Greatest Common Divisor (GCD) and how to find it for a given numerator and denominator. Emphasize the importance of dividing both by the GCD to simplify the fraction. Provide several examples of fractions that need simplifying and walk through the process step by step. Encourage students to always check their work to ensure the fraction is in its lowest terms. As an activity, have students find and simplify fractions from their textbooks or create their own fractions to simplify.

Practice Makes Perfect: Simplifying Fractions – Let’s simplify fractions together – Work through class examples – Example: Simplify 4/8 to 1/2 by dividing by the GCD of 4 – Discuss questions and challenges – Open discussion helps clarify doubts – Practice makes mastery | This slide is designed to engage the class in a collaborative exercise to simplify fractions. Start by explaining the process of finding the greatest common divisor (GCD) and how it’s used to reduce fractions to their lowest terms. Work through several examples as a class, encouraging participation from the students. As you go through the examples, pause to address any questions or challenges that arise, ensuring that all students are following along. Emphasize the importance of practice in mastering the concept of simplifying fractions. The goal is for students to feel comfortable with the process and to understand the reasoning behind it. For homework, assign additional problems for further practice.

Real-Life Applications of Simplified Fractions – Importance of simplifying fractions – Simplification in cooking and building – Halving a recipe or measuring lengths precisely – Using fractions while shopping – Comparing prices, calculating discounts – Activity: Make simplified fractions – Choose everyday items, write fractions, simplify them | Understanding how to simplify fractions is crucial not just in math class, but in everyday life. It helps in cooking when adjusting recipes, in building to measure materials accurately, and in shopping to understand prices and discounts. For the activity, students will select common items or scenarios, write down the fractions involved, and practice simplifying them. This will help them see the practical use of fractions. Teachers should prepare examples like cutting a recipe in half (1/2 of 2/4 cups of sugar) or finding the best buy (1/3 off of $15 vs. 1/4 off of $20). Encourage creativity and real-world connections.

Class Activity: Fraction Simplification Race – Teams compete to simplify fractions – Apply learned methods to win – Prizes for top simplifying teams – Encourages teamwork and learning | This activity is designed to reinforce the concept of simplifying fractions in a fun and competitive environment. Divide the class into small teams, ensuring a mix of abilities in each group. Provide each team with a set of fractions to simplify. Review the methods for finding the greatest common divisor (GCD) and how to divide the numerator and denominator by the GCD to write fractions in lowest terms. Set a timer and let the race begin! Monitor the teams, offering guidance as needed. At the end of the activity, review the correct simplifications and award prizes to the teams with the most correct answers. This will help students to solidify their understanding of the topic while also promoting teamwork and healthy competition.

Wrapping Up: Fractions in Lowest Terms – Recap: Simplifying Fractions – Homework: 10 Fractions to Simplify – Find the greatest common divisor (GCD) for each and write in lowest terms. – Next Class: Add & Subtract Fractions – Review adding and subtracting fractions for our next lesson. – Practice Makes Perfect! – Keep practicing to master simplifying fractions! | As we conclude today’s lesson on simplifying fractions, remind students of the importance of finding the greatest common divisor (GCD) to write fractions in their lowest terms. For homework, they should simplify 10 different fractions, ensuring they understand the process. Looking ahead, students should start to familiarize themselves with the concepts of adding and subtracting fractions to be prepared for the next class. Encourage them to practice regularly, as this will help solidify their understanding of fractions and build a strong foundation for more complex operations.