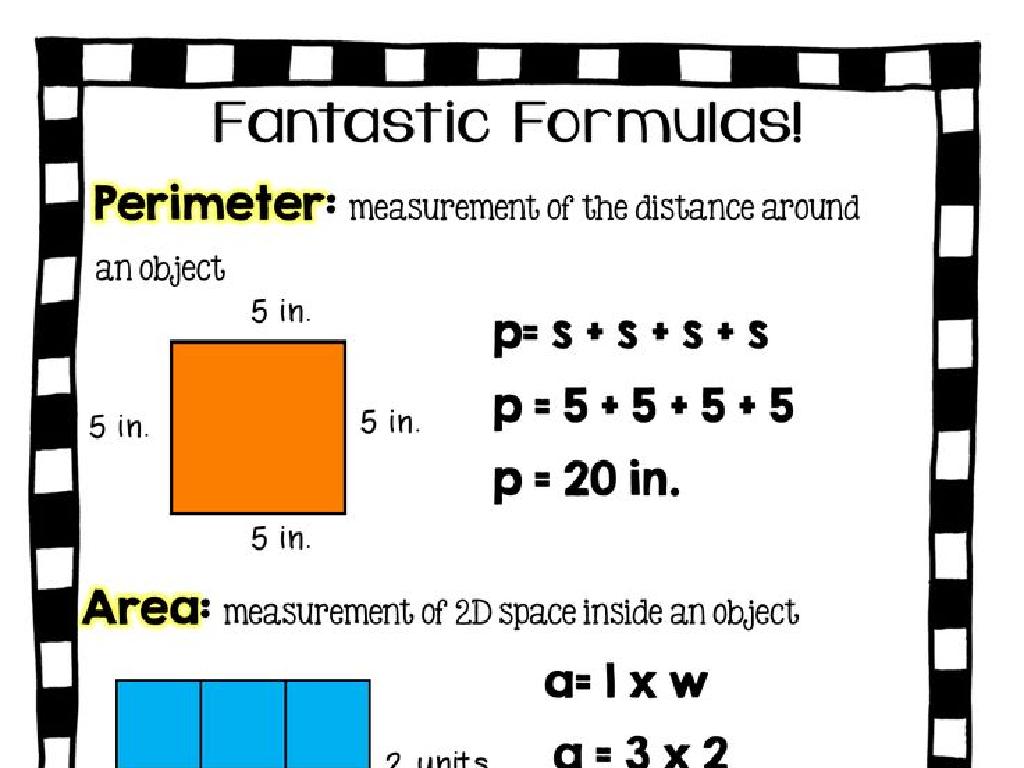
Rate Of Change: Graphs
Subject: Math
Grade: Eighth grade
Topic: Interpret Functions
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Welcome to Rate of Change!
– Understanding rate of change
– It’s the speed at which a variable changes over a specific period of time.
– Real-life rate of change examples
– Examples: Speed of a car, growth of a plant.
– Exploring graphs and functions
– How graphs can show the rate at which things change.
– Preview of today’s lesson
|
This slide introduces the concept of rate of change, which is a fundamental idea in understanding how variables interact over time. It’s important to relate this mathematical concept to real-life situations to help students grasp its practical applications. For instance, the speed of a car or the growth of a plant can be represented and analyzed using rate of change. Today’s lesson will focus on how this concept is represented in graphs and functions, setting the stage for students to learn how to interpret and calculate the rate of change from graphical data. Encourage students to think of other examples where they encounter rates of change in their daily lives.
Understanding Rate of Change
– Define Rate of Change
– It measures how one quantity changes in relation to another quantity.
– Formula: Change in Value over Time
– If a car travels 60 miles in 2 hours, the rate is 30 miles per hour.
– Example: Car Speed
– Speed is the rate at which the car’s position changes over time.
– Example: Plant Growth
– If a plant grows 5 inches in 10 days, the rate is 0.5 inch per day.
|
The rate of change is a fundamental concept in understanding how variables interact over time. It’s the speed at which one quantity changes relative to another. For instance, when we talk about the speed of a car, we’re referring to the rate of change of distance over time. Similarly, when we measure how quickly a plant grows, we’re looking at the rate of change of its height over time. This slide aims to solidify the students’ understanding of the rate of change by using relatable examples and applying the formula for rate of change. Encourage students to think of other examples where they can observe the rate of change in their daily lives.
Graphs and Rate of Change
– Identifying rate of change
– Rate of change is the slope of the line on a graph.
– Positive vs. negative rates
– Positive slope goes up, negative slope goes down.
– Understanding zero rate of change
– Zero rate means constant value; the graph is a flat line.
– Graph interpretation practice
|
This slide introduces the concept of rate of change in the context of graph interpretation. Students will learn to identify the rate of change by looking at the slope of the line on a graph. A positive rate of change indicates an increase in the y-value as the x-value increases, represented by an upward-sloping line. Conversely, a negative rate of change shows a decrease, with the line sloping downward. A zero rate of change means there is no change in the y-value as the x-value increases, which is shown as a horizontal line on the graph. Encourage students to practice by looking at different graphs and determining the rate of change, discussing what these rates represent in real-world situations.
Calculating Rate of Change
– Understanding slope formula
– Slope formula: (y2 – y1) / (x2 – x1) represents rate of change between two points.
– Practice problem on rate of change
– Example: Calculate the rate of change for points (3, 7) and (6, 1).
– Meaning of different slopes
– Positive slope means increase, negative slope means decrease, zero slope means no change.
– Real-world application of slopes
|
This slide introduces the concept of rate of change in the context of graphing functions, focusing on the slope formula as a tool for calculation. Start by explaining the slope formula and its components, emphasizing that it represents the rate at which y changes with respect to x. Provide a practice problem for students to apply the formula and find the rate of change between two points on a graph. Discuss the significance of different slopes: positive slopes indicate an upward trend, negative slopes indicate a downward trend, and a zero slope indicates a constant function. Finally, relate the concept to real-world scenarios, such as speed being the rate of change of distance over time, to help students understand the practical applications of slopes in interpreting functions.
Real-World Applications of Rate of Change
– Economics: Stock market trends
– Analyze graphs to predict financial growth or decline
– Science: Chemical reaction rates
– Observe how reaction rates vary over time
– Everyday life: Comparing object speeds
– Determine which object moves faster
– Understanding rate of change
|
This slide aims to show students how the concept of rate of change is applied in various real-world scenarios. In economics, students can learn how to interpret stock market graphs to understand trends and make predictions. In science, they can analyze graphs to observe the rates at which chemical reactions occur. For everyday life applications, comparing the speeds of different objects can help students grasp the concept of velocity. Emphasize that the rate of change is a universal concept that helps us quantify and understand changes over time in diverse fields. Encourage students to think of other areas where rate of change might be important and to bring examples to the next class.
Class Activity: Graphing Race!
– Form small groups for a challenge
– Calculate rate of change
– Use the formula (change in value) / (change in time)
– Present findings to class
– Discuss real-world significance
– How does this apply to everyday situations?
|
This interactive class activity is designed to help students understand the concept of rate of change through hands-on learning. Divide the class into small groups and provide each with a different graphing challenge that involves calculating the rate of change. This could involve scenarios such as temperature changes over a week, speed of a car during a trip, or growth of a plant. After calculations, each group will present their graph and findings, explaining how the rate of change is significant in real-world contexts. For the teacher: Prepare diverse scenarios, ensure each group understands the task, and facilitate discussions post-presentations. Encourage students to think critically about how the rate of change is observed and measured in various aspects of life.
Wrapping Up: Rate of Change
– Recap: What is Rate of Change?
– It’s the measure of how one quantity changes in relation to another
– Why Rate of Change matters
– Helps understand real-world phenomena like speed
– Homework: Worksheet completion
– Practice problems to solidify today’s lesson
– Next class: Intro to Functions
– Get ready to explore the world of functions!
|
As we conclude today’s lesson, remind students that the rate of change is a fundamental concept in understanding how different quantities are related in both math and the real world, such as speed or growth over time. For homework, students should complete the provided worksheet to practice calculating the rate of change from various graphs. This will help reinforce their understanding and prepare them for the upcoming lesson on functions. Make sure to check for comprehension and answer any questions before they leave. Next class, we will begin our journey into functions, which are vital for understanding complex relationships in mathematics.

/early_republic_us_history.jpg)