Your next great Lessn starts here.

Introduction to Multiplication – Recap: What is multiplication? – Multiplication as repeated addition – If we add 4 three times, it’s 4+4+4, which is 12 – One-digit multiplication examples – Examples: 3×4, 2×5, and 6×7 – Practice with simple problems – Try solving 4×3 and 5×2 on your own! | Begin the lesson by recapping the concept of multiplication, ensuring that students remember it as a method for finding the total number of items in groups of the same size. Emphasize that multiplication is essentially repeated addition, which is a more efficient way of adding the same number several times. Provide clear examples of one-digit multiplication, such as 3×4, 2×5, and 6×7, and demonstrate how these can be solved by adding the number to itself repeatedly. Encourage students to practice with simple problems to solidify their understanding, and prepare to assist them with any challenges they encounter. This foundation will be crucial as they learn to use the distributive property in multiplication.

The Distributive Property in Multiplication – What is the Distributive Property? – It lets you multiply a sum by multiplying each addend separately and then add the products. – Breaking up numbers with Distributive Property – For example, 6 x 7 can be broken into (6 x 5) + (6 x 2). – The usefulness of Distributive Property – It simplifies multiplication, especially with larger numbers. – Practice with Distributive Property | Introduce the Distributive Property as a method to simplify multiplication by breaking it into smaller, more manageable parts. Explain that it allows us to multiply each part of a sum separately and then add the results together. Use examples to show how to break up numbers, such as turning 6 x 7 into (6 x 5) + (6 x 2) to make it easier to multiply in their heads or on paper. Discuss why this property is useful, particularly when dealing with larger numbers or when mental math is needed. Conclude with practice problems to reinforce the concept, ensuring students understand how to apply the Distributive Property in different scenarios.

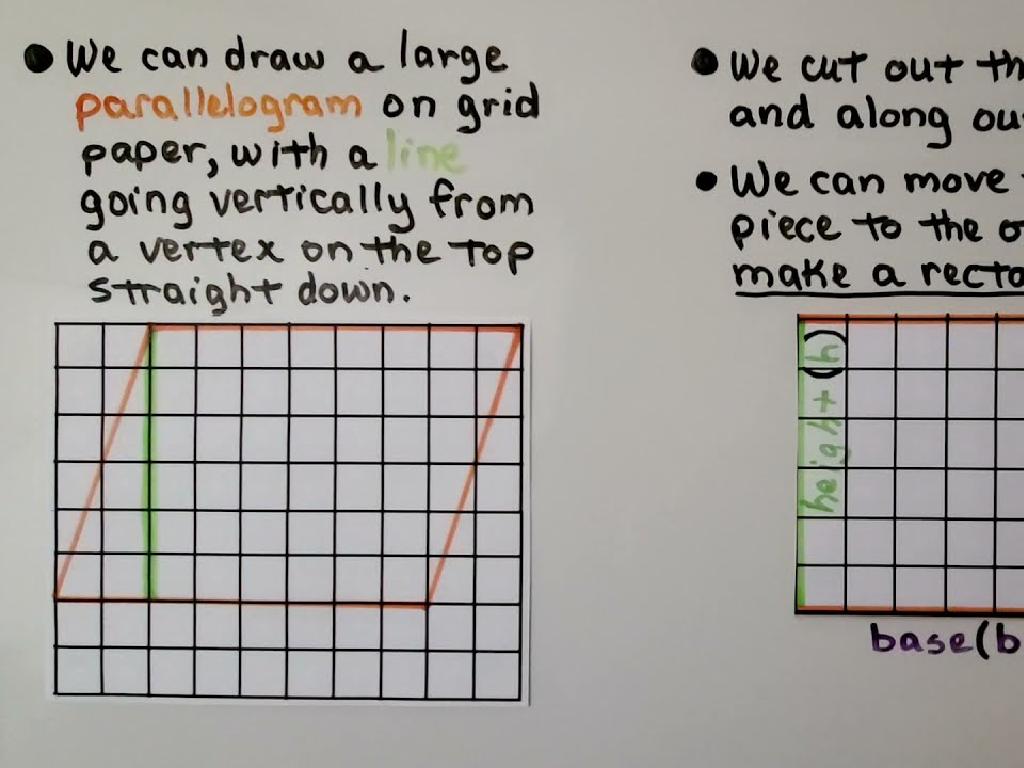
Applying the Distributive Property – Steps to multiply using distributive property – Break a number into parts, multiply each by the other number, then add the products. – Example: 6 x 7 as 6 x (5 + 2) – 6 x 5 = 30 and 6 x 2 = 12, so 6 x 7 = 30 + 12 – Visualize distribution with objects – Use blocks or drawings to show 6 groups of 5 and 6 groups of 2. – Combine products for the final answer – Add the two products together to find 6 x 7. | Introduce the concept of the distributive property as a way to simplify multiplication by breaking one of the numbers into smaller, more manageable parts. Use the example of 6 x 7 to show how 7 can be split into 5 and 2, making two easier multiplication problems: 6 x 5 and 6 x 2. Provide a visual representation, such as blocks or a drawing, to help students see how the numbers are distributed and then combined to reach the final product. This visual aid reinforces the concept and helps students understand how to apply the distributive property to multiplication problems. Encourage students to practice with different numbers and to draw their own visual representations.

Practice: Distributive Property in Multiplication – Solve problems using distributive property – e.g., 6 x 7 can be broken into (6 x 5) + (6 x 2) – Work through examples with the teacher – Teacher demonstrates, then students try – Explore different ways to break up numbers – Break 9 x 4 into (9 x 2) + (9 x 2) or (9 x 3) + (9 x 1) – Understand how distribution simplifies multiplication – It helps to manage larger numbers easily | This slide is aimed at providing students with practice problems to apply the distributive property in multiplication. Begin by explaining the concept with a simple example and solve it step by step. Encourage students to participate in solving the problems and guide them through the process. Discuss the different strategies for breaking up numbers, such as by place value or by making easier-to-multiply pairs. Emphasize that the distributive property is a useful tool for simplifying complex multiplication problems, especially when dealing with larger numbers. Provide a variety of problems for the students to work on and ensure to give feedback on their approach and solutions.

Group Activity: Exploring Distributive Property – Form small groups for problem-solving – Solve problems using Distributive Property – Break larger multiplication into smaller, easier problems – Present your group’s strategy – Share how you distributed the numbers with the class – Discuss the variety of strategies used – Learn from each group’s approach and understand different methods | This group activity is designed to encourage collaborative learning and to deepen students’ understanding of the Distributive Property in multiplication. Have the students form small groups and provide them with a set of multiplication problems. Each group should use the Distributive Property to solve the problems by breaking them down into smaller, more manageable parts. After solving, each group will present their method to the class, explaining how they distributed the numbers. Following the presentations, lead a class discussion on the different strategies used, highlighting the benefits of each approach. This will help students see the practical application of the Distributive Property and learn from their peers. Possible activities: 1) Multiplying two-digit by one-digit numbers, 2) Using arrays to visualize distribution, 3) Creating word problems that apply the Distributive Property, 4) Peer-teaching where students explain the concept to each other, 5) Using manipulatives to demonstrate the property physically.

Class Activity: Crafting Multiplication Problems – Create your own multiplication problems – Use the Distributive Property to solve – Break larger numbers into smaller parts to make multiplying easier – Partner up to share your problems – Solve your partner’s problems together | This activity is designed to reinforce the concept of the distributive property in multiplication. Students will create their own multiplication problems, which encourages them to engage with the material actively. They will then apply the distributive property to solve these problems, breaking down larger numbers into more manageable parts. For example, multiplying 6 by 7 can be broken down into (6×5) + (6×2). After creating and solving their problems, students will pair up to exchange and solve each other’s problems, promoting collaboration and peer learning. As a teacher, circulate the room to assist with problem creation and ensure students are correctly applying the distributive property. Possible activities for different students could include creating word problems, drawing arrays to visualize the problems, or using manipulatives to represent the equations physically.

Review and Reflect: Distributive Property – Recap today’s key points – Discuss the Distributive Property – Distributive Property breaks down complex multiplication – Reflect on its multiplication benefits – Simplifies larger numbers into manageable parts – Consider real-world applications – Useful in everyday math, like shopping and budgeting | As we conclude today’s lesson, let’s review the key concepts we’ve covered about using the distributive property in multiplication. We’ve learned that this property allows us to break down a multiplication problem into smaller, more manageable parts, making it easier to solve without a calculator. Understanding this method is crucial as it not only simplifies complex multiplication but also lays the foundation for algebraic thinking. Reflect on how this approach can be applied in real-life scenarios, such as calculating the cost of multiple items while shopping or planning a budget. Encourage students to think of other situations where they can apply the distributive property and share their ideas in the next class.

Homework: Practice the Distributive Property – Practice multiplication with Distributive Property – Break larger problems into smaller, easier ones – Complete the multiplication worksheet – Use the worksheet to apply what you’ve learned – Study for the upcoming multiplication quiz – Review today’s lesson to prepare for the quiz | This homework assignment is designed to reinforce today’s lesson on the distributive property of multiplication. Students should practice breaking down larger multiplication problems into smaller, more manageable parts using the distributive property. The provided worksheet will give them a chance to apply this technique. Encourage students to review their class notes and any in-class examples to prepare for the quiz on multiplication in the next class. Offer some strategies for studying, such as creating flashcards or practicing with a family member. Remind students that understanding the distributive property will make multiplication easier and is a skill they will use in higher-level math.