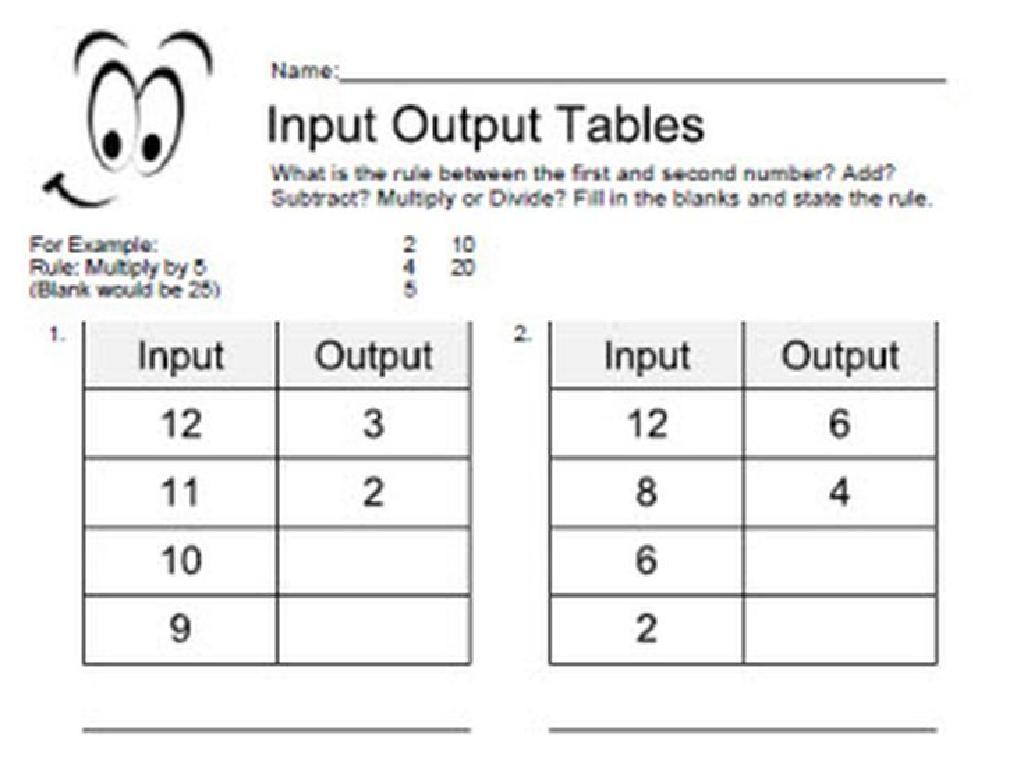
Complete The Fraction Multiplication Sentence I
Subject: Math
Grade: Fifth grade
Topic: Multiply Fractions
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Today’s Adventure: Multiplying Fractions!
– Fractions represent parts
– Imagine a pizza cut into equal slices; each slice is a fraction of the pizza.
– Multiplication of fractions
– When we multiply fractions, we’re finding a part of a part.
– Visualizing fraction multiplication
– Picture multiplying 1/2 of a pizza by 1/3; we only get 1/6 of the pizza.
– Effect on fraction size
|
Begin by explaining that fractions are a way to represent parts of a whole, using everyday examples like slices of pizza. Then, introduce the concept of multiplying fractions as finding a part of a part, which can be a new and exciting way to look at multiplication for fifth graders. Use visual aids to help students understand how multiplying two fractions results in a smaller fraction, as it’s like taking a smaller piece of an already small piece. Emphasize that multiplication can make fractions smaller, not just bigger like with whole numbers. Encourage students to visualize the process to better grasp the concept.
Understanding Fraction Multiplication
– Combining parts of parts
– Doubling recipes or sharing pizza
– Visualize using fraction bars
– Fraction bars help see the parts combined
– Example: 1/2 x 1/3
– 1/2 of a 1/3 bar shows the new fraction
|
This slide introduces the concept of multiplying fractions to fifth graders by relating it to familiar activities such as doubling a recipe or dividing a pizza among friends. Emphasize that when we multiply fractions, we are essentially finding a part of a part. Use fraction bars as a visual aid to help students understand how fractions are multiplied. Show how multiplying 1/2 by 1/3 can be visualized by covering half of a bar divided into thirds, which demonstrates the concept in a tangible way. Encourage students to draw their own fraction bars to solve multiplication problems and to think of other real-life examples where they might multiply fractions.
Multiplying Whole Numbers by Fractions
– Understanding multiplication with fractions
– Multiplying a whole number by a fraction
– It’s like finding a part of the whole number
– Example: 3 x 1/4 of pizzas
– 3 x 1/4 means 1/4 part of 3 pizzas
– Visualizing with a drawing
– Let’s draw to see what 1/4 of 3 looks like
|
This slide introduces the concept of multiplying whole numbers by fractions, which is essentially finding a part of the whole number. Use the example of pizza to make the concept relatable if we have 3 pizzas and we want to find what 1/4 of these pizzas would be, we multiply 3 by 1/4. Encourage students to visualize the process by drawing it out. They can draw 3 pizzas and then shade in 1/4 of each pizza to find the answer. This visual representation will help solidify their understanding of the concept. During the class, walk through the drawing process step by step, and then allow the students to try with different numbers and fractions.
Multiplying Fractions by Fractions
– Multiply numerators together
– Multiply denominators together
– Example: 1/2 x 3/4
– 1/2 x 3/4 = (1×3)/(2×4) = 3/8
– Visualize using area models
– Draw a rectangle, divide into 4, shade 3
|
This slide introduces the concept of multiplying fractions by fractions to fifth graders. Start by explaining that to multiply fractions, we multiply the numerators (top numbers) to get the new numerator and multiply the denominators (bottom numbers) to get the new denominator. Use the example 1/2 x 3/4 to illustrate this point. Show how 1/2 x 3/4 equals 3/8 by multiplying 1 by 3 and 2 by 4. Then, demonstrate how to visualize the multiplication using an area model. Draw a rectangle, divide it into 4 equal parts to represent 3/4, and then shade in 1/2 of those parts to show the product of 3/8. This visual representation helps students grasp the concept of fraction multiplication more concretely.
Completing Fraction Multiplication Sentences
– Fill in the missing fraction
– Example: 2/3 x ___ = 2/9
– Find the fraction that completes the equation
– Determine the multiplier
– How do we find a number that multiplies with 3 to get 9?
– Solve: What times 3 equals 9?
– The missing fraction is 1/3 because 3 x 1/3 equals 1
|
This slide is aimed at helping students practice how to complete a fraction multiplication sentence by finding the missing fraction. Start with an example like 2/3 x ___ = 2/9 and guide the students to think about the relationship between the denominator of the known fraction (3) and the denominator of the product (9). They should recognize that they need to multiply 3 by a number to get 9, which is 3. Therefore, the missing fraction is 1/3 because when 3 is multiplied by 1/3, the result is 1, and 2/3 times 1/3 equals 2/9. Encourage students to use this method to find missing fractions in other multiplication sentences and to be ready to share their methods and answers in the next class.
Fraction Multiplication Practice
– Multiply fractions step by step
– Simplify fractions when possible
– Practice Problem 1: 2/5 x 1/2
– Find the product of numerators and denominators
– Practice Problem 2: 4/7 x 3/4
– Find the product of numerators and denominators
|
This slide is designed to provide students with practice problems for multiplying fractions. Start by explaining the steps to multiply fractions: multiply the numerators (top numbers) to get the new numerator, and multiply the denominators (bottom numbers) to get the new denominator. Then, simplify the fraction if possible. For the first problem, 2/5 x 1/2, the solution is 2/10, which simplifies to 1/5. For the second problem, 4/7 x 3/4, the solution is 12/28, which simplifies to 3/7. Encourage students to work through these problems and simplify their answers. Provide guidance on how to simplify fractions and remind them to always look for the greatest common divisor. This exercise will help reinforce their understanding of fraction multiplication and the importance of simplification.
Class Activity: Fraction Multiplication Art
– Create fraction multiplication art
– Choose two fractions to multiply
– Color the grid to show the answer
– Use different colors to represent each fraction
– Share your art with the class
– Explain how the colored sections represent the product
|
This activity is designed to help students visualize the concept of multiplying fractions. Provide each student with a grid and colored pencils or crayons. Students will select two fractions and color in the appropriate sections of the grid to represent each fraction. When they overlap the colored sections, the intersecting area will represent the product of the two fractions. This hands-on activity not only reinforces the concept of fraction multiplication but also allows for creativity. Possible variations include using different shapes or creating a class mural. Encourage students to explain their reasoning and how their art represents the multiplication of fractions.
Wrapping Up: Fraction Multiplication
– Excellent work with fractions!
– Homework: Fraction multiplication worksheet
– Complete the problems to reinforce today’s lesson
– Practice is key to mastery
– The more you practice, the better you’ll understand
– Keep up the great effort!
|
Today’s lesson focused on multiplying fractions, a crucial skill in mathematics. The homework assignment is a worksheet designed to reinforce the concepts learned in class. Encourage students to take their time with each problem and to remember the steps we’ve practiced: multiply the numerators, multiply the denominators, and simplify if possible. Remind them that practice is essential in becoming comfortable with multiplying fractions and that they should try their best on each problem. Offer to answer any questions in the next class about the homework or any part of today’s lesson.