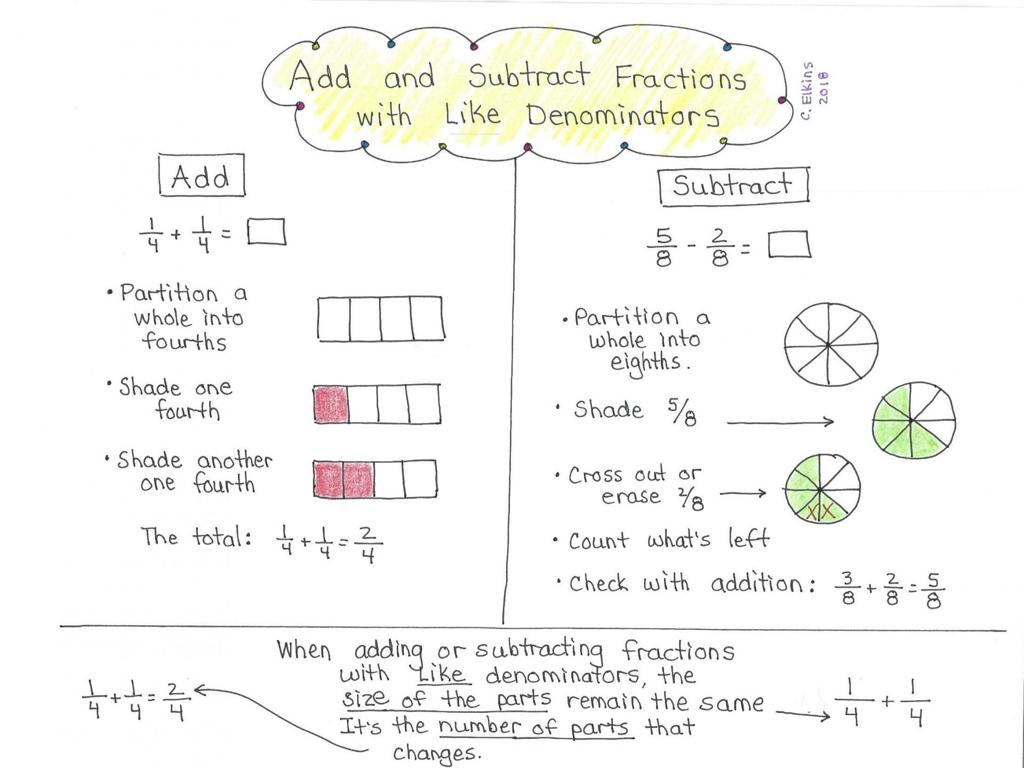
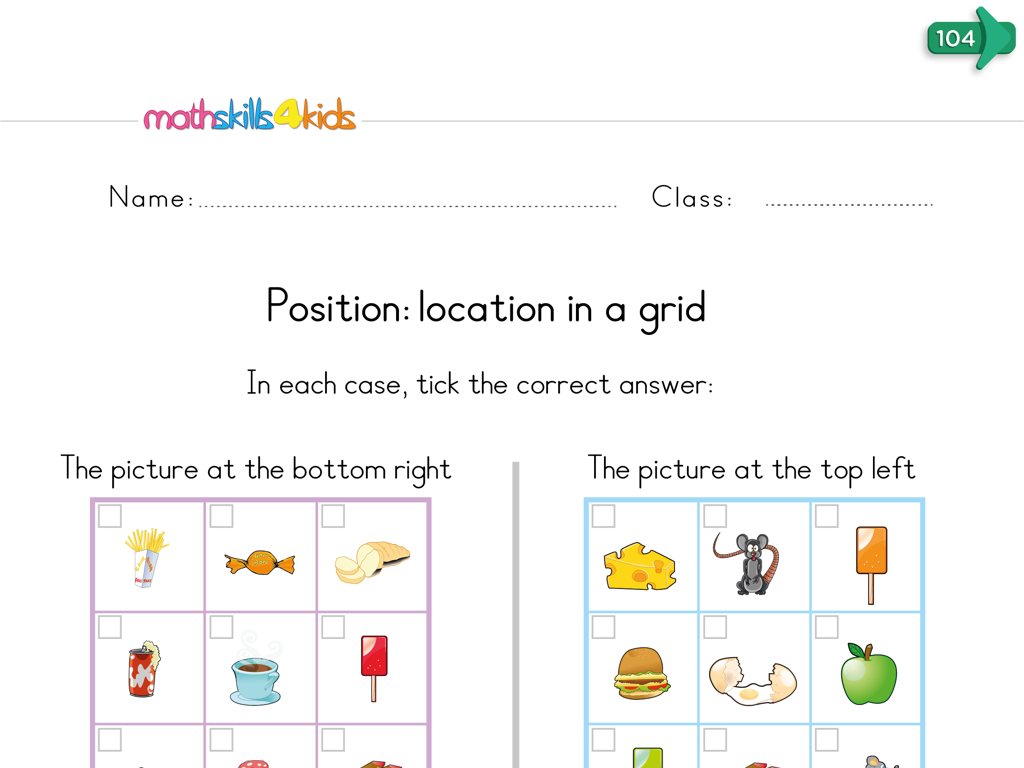
Gcf And Lcm: Word Problems
Subject: Math
Grade: Seventh grade
Topic: Number Theory
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Exploring GCF and LCM in Number Theory
– GCF: Greatest Common Factor
– The largest number that divides two or more numbers without a remainder.
– LCM: Least Common Multiple
– The smallest number that is a multiple of two or more numbers.
– Building blocks of numbers
– GCF and LCM in daily life
– Scheduling, electronics, construction use GCF and LCM for efficiency.
|
Today’s lesson will dive into the concepts of Greatest Common Factor (GCF) and Least Common Multiple (LCM), which are fundamental in understanding the structure and relationships between numbers. GCF is crucial when simplifying fractions or finding common denominators, while LCM is used in adding or subtracting fractions with different denominators. Real-life applications include solving problems related to scheduling events, optimizing electronic circuitry, or planning construction projects where measurements need to align. Encourage students to think of scenarios where GCF and LCM could be applied. Provide word problems that require the use of GCF and LCM to solve. This will help students see the practical value of these concepts beyond the classroom.
Understanding GCF in Word Problems
– GCF stands for Greatest Common Factor
– Largest number dividing two or more numbers
– Example: GCF of 12 and 16
– The biggest number that both 12 and 16 can be divided by is 4
– Application in solving problems
– Use GCF to simplify fractions or find how many groups of items can be made
|
GCF, or Greatest Common Factor, is a foundational concept in number theory and is particularly useful in solving various mathematical problems, including word problems. It is the largest number that can evenly divide two or more numbers without leaving a remainder. For instance, the GCF of 12 and 16 is 4, because 4 is the largest number that can divide both 12 and 16 evenly. Understanding GCF allows students to simplify fractions to their lowest terms and solve problems that involve grouping items into larger groups. Encourage students to practice by finding the GCF of different sets of numbers and applying this knowledge to real-world scenarios.
Finding the Greatest Common Factor (GCF)
– List all factors of each number
– Factors of 18: 1, 2, 3, 6, 9, 18
– Spot the common factors
– Common factors of 18 and 24: 1, 2, 3, 6
– Select the largest common factor
– The GCF of 18 and 24 is 6
– Apply GCF to solve problems
– Use GCF to simplify fractions like 18/24 to 3/4
|
This slide introduces the concept of finding the Greatest Common Factor (GCF) of two or more numbers, which is a foundational skill in number theory and essential for solving various mathematical problems, including simplifying fractions and solving word problems involving divisibility. Start by listing the factors of each given number, then identify which factors are common to all the numbers. The greatest of these common factors is the GCF. Provide examples with different sets of numbers to ensure students understand the process. Encourage students to practice by finding the GCF of numbers provided in class and as homework.
Understanding Least Common Multiple (LCM)
– Define LCM
– Least Common Multiple, the smallest shared multiple
– LCM’s role in number theory
– Example: LCM of 3 and 4
– Smallest number divisible by both 3 and 4 is 12
– Applying LCM to word problems
– Use LCM to solve problems involving repeated events
|
LCM, or Least Common Multiple, is a foundational concept in number theory, particularly useful when dealing with fractions, ratios, and periodic events. It’s the smallest number that two or more numbers can divide into without leaving a remainder. For example, the LCM of 3 and 4 is 12, which is the smallest number that both 3 and 4 can divide into evenly. In word problems, LCM can be applied to find out how often two events with different cycles coincide, such as determining a schedule for two buses that arrive at different intervals. Encourage students to practice by finding the LCM of various pairs of numbers and applying this knowledge to solve real-world problems.
Finding the Least Common Multiple (LCM)
– List multiples of each number
– For 4 and 5, list 4, 8, 12, 16, 20 and 5, 10, 15, 20, 25
– Spot the common multiples
– Look for multiples that appear in both lists
– Select the smallest shared multiple
– The LCM of 4 and 5 is 20, as it’s the smallest number in both lists
– Apply LCM to solve problems
|
This slide introduces the concept of finding the Least Common Multiple (LCM) through a systematic approach. Start by listing a set of multiples for each number involved in the problem. Then, guide students to identify the multiples that are common to each list. Emphasize the importance of choosing the smallest of these common multiples, as this is the LCM. Provide examples with small numbers to ensure understanding, and then apply this method to solve word problems that involve finding the LCM, such as determining the next time two events with different cycles will coincide. Encourage students to practice with additional examples and to recognize the practical applications of LCM in real-life scenarios.
GCF and LCM: Solving Real-World Problems
– Apply GCF and LCM in real scenarios
– Find the greatest common factor (GCF) to divide things into smaller sections.
– Comprehend the context of problems
– Grasp the story or situation in the problem to find clues.
– Determine when to use GCF or LCM
– Use GCF for shared attributes; LCM for repeated events.
– Practice with example word problems
– Example: Scheduling events or dividing resources.
|
This slide aims to help students understand the practical applications of GCF (Greatest Common Factor) and LCM (Least Common Multiple) in solving real-world problems. Students should learn to analyze the context of a problem to decide whether to use GCF or LCM. GCF is used when the goal is to break things down into smaller, equal parts, such as dividing a set of items into groups. LCM is used when dealing with events that repeat over a period, such as finding the least time interval for two events to coincide. Provide students with word problems that require them to apply GCF and LCM, ensuring they understand the reasoning behind choosing one over the other. Encourage them to explain their thought process when solving these problems.
GCF Word Problem: Balloon Bunches
– Sarah’s balloon counts: 15 red, 20 blue
– Determine bunch size without mixing
– Find the GCF of 15 and 20
– GCF of 15 and 20 is 5
– GCF is the largest bunch size possible
– Each bunch will have 5 balloons
|
This slide presents a word problem involving the Greatest Common Factor (GCF). Sarah has two sets of balloons and wants to create bunches of each color without mixing them. To find the largest possible equal-sized bunches, students must calculate the GCF of 15 and 20. The GCF is the highest number that divides both 15 and 20 without a remainder, which in this case is 5. Therefore, Sarah can make bunches of 5 balloons each. This example helps students apply their understanding of GCF to solve real-world problems. Encourage students to work through the problem step-by-step and verify their answer by checking if 5 is indeed the largest number that divides both 15 and 20.
GCF and LCM: Race Track Problem
– Analyze the race track problem
– Identify numbers: 75s and 60s laps
– Two runners with different lap times
– Find the LCM of 75 and 60
– LCM(75, 60) gives the time they align
– Determine meeting time
– Calculate when runners meet at start
|
This slide presents a word problem involving finding the Least Common Multiple (LCM) to determine when two runners will meet at the starting point again. Students should first identify the key numbers to compare, which are the lap times of the runners. Then, they need to find the LCM of these numbers to solve the problem, as it represents the smallest time interval in which both runners’ laps will align. The LCM of 75 and 60 is 300 seconds, meaning after 300 seconds, both runners will be at the starting point together. This exercise helps students apply their understanding of LCM to real-world scenarios and enhances their problem-solving skills.
Class Activity: Find Your Match!
– Receive a card with a number
– Find a partner with a related number
– Calculate GCF or LCM together
– Use methods like prime factorization or Euclidean algorithm
– Explain the reasoning behind your answer
– Discuss how you found the common factors or multiples
|
This interactive activity is designed to help students practice finding the Greatest Common Factor (GCF) and Least Common Multiple (LCM) in a collaborative and engaging way. Each student will receive a card with a number on it. Their task is to find another student with a number that shares a GCF or LCM with theirs. Once pairs are formed, they will work together to calculate the GCF or LCM of their two numbers, using methods such as listing out factors, prime factorization, or the Euclidean algorithm. After calculating, students should explain their reasoning and the steps they took to arrive at their answer. This activity encourages peer learning and helps reinforce the concepts of GCF and LCM through practice. For the teacher: Prepare sets of cards with numbers that have clear GCFs or LCMs. Consider creating a few challenging pairs to differentiate for advanced students. Have a list of possible pairs and their GCFs or LCMs ready for quick reference during the activity.
Wrapping Up: GCF and LCM
– Recap GCF and LCM concepts
– Real-world application of GCF and LCM
– GCF helps in dividing things evenly, LCM in planning events or purchases
– Homework: Practice with word problems
– Solve problems to strengthen understanding
– Be prepared to discuss solutions
– Share how you solved the problems in the next class
|
As we conclude today’s lesson, remind students of the key concepts of Greatest Common Factor (GCF) and Least Common Multiple (LCM) and their significance in solving various mathematical problems. Emphasize how these concepts are not just theoretical but have practical applications in everyday life, such as in dividing resources equally or scheduling events with no conflicts. Assign a set of word problems as homework to reinforce their understanding, and encourage students to be ready to discuss the strategies they used to find solutions in the next class. This will help them not only to remember the methods but also to learn from each other’s approaches.