Your next great Lessn starts here.

Exploring Greatest Common Factor (GCF) – What is the Greatest Common Factor? – The largest number that divides two or more numbers without a remainder. – Building blocks: Prime factors – Prime factors are the ‘building blocks’ that multiply to create numbers. – GCF’s role in math and life – GCF simplifies fractions, finds common denominators, and solves real-world problems. – Methods to find the GCF – Use prime factorization or Euclidean algorithm to find GCF. | This slide introduces the concept of the Greatest Common Factor (GCF), a fundamental topic in number theory. GCF is the highest number that can divide two or more integers without leaving a remainder. Understanding prime factors is crucial as they are the basic elements that make up all numbers. Emphasize the practicality of GCF in simplifying fractions, determining common denominators, and its applications in problem-solving scenarios such as sharing items equally. Teach students different methods to find the GCF, including prime factorization and the Euclidean algorithm, ensuring they grasp the concept through examples and practice problems.

Understanding Factors – Define a factor – A factor is a number that divides another without leaving a remainder. – Explore factors up to 50 – List factors for numbers 1-50, e.g., factors of 12 are 1, 2, 3, 4, 6, 12. – Identify factors via multiplication – Use multiplication to find factors: if 4 x 3 = 12, then 4 and 3 are factors of 12. – Practice finding factors | Begin the lesson by defining what a factor is and its role in mathematics. Explain that factors are the building blocks of numbers and are essential for understanding division and multiplication. Provide a chart or list of numbers up to 50 and their factors to help students visualize the concept. Demonstrate how multiplication is used to identify factors by showing that if two numbers multiply to give another number, they are factors of that number. Include practice exercises where students list factors of given numbers to reinforce the concept. This foundational knowledge will be crucial for learning about the greatest common factor.

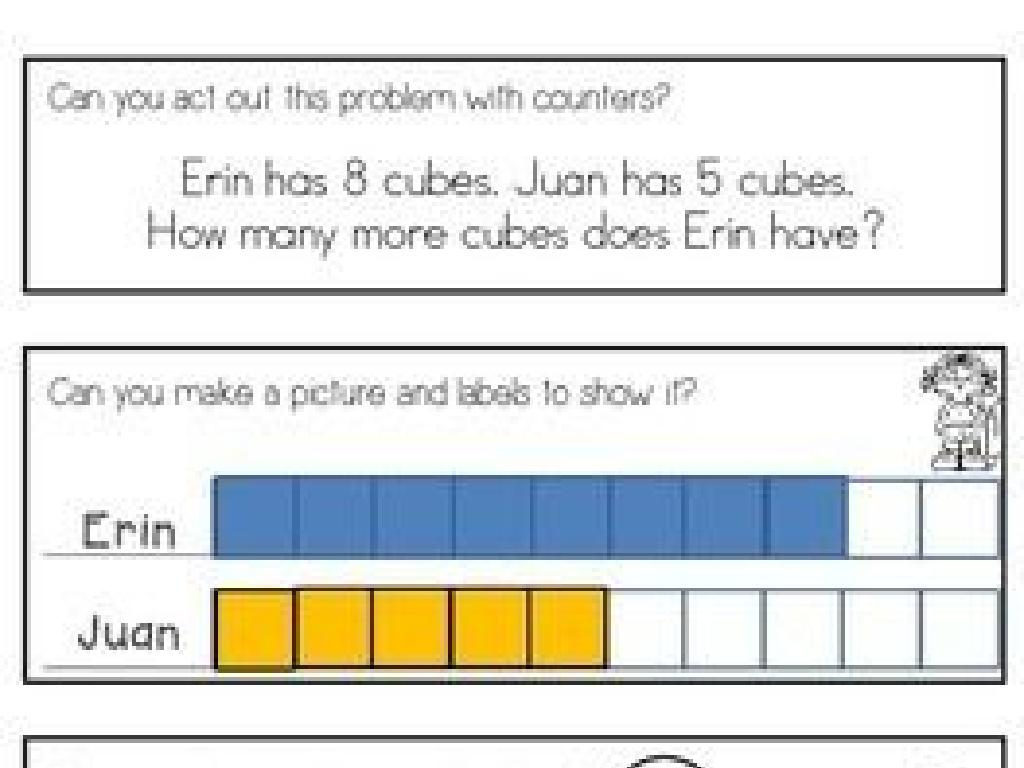
Finding Common Factors – Understanding common factors – Numbers that divide two or more numbers without a remainder. – Venn diagrams and common factors – Use circles to represent factors of numbers and find overlaps. – Example: Factors of 24 and 36 – 24 and 36 share factors 1, 2, 3, 4, 6, and 12. – Practice finding common factors | Begin by explaining that common factors are numbers that exactly divide two or more numbers with no remainder left. Introduce Venn diagrams as a visual tool to help students identify common factors by representing each number’s factors in overlapping circles. Use the example of 24 and 36 to show how to list out factors and find the common ones. Encourage students to practice with different numbers to solidify their understanding. This will prepare them for learning about the greatest common factor.

Exploring the Greatest Common Factor – What is GCF? – The largest number that divides two or more numbers without a remainder. – GCF’s role in fractions – GCF helps reduce fractions to their simplest form. – GCF in daily life – Used in splitting things into smaller sections, like sharing equally among friends. – Simplifying with GCF | The Greatest Common Factor, or GCF, is a fundamental concept in number theory and an essential tool for simplifying fractions. Understanding GCF allows students to reduce fractions to their simplest form, making calculations easier and more intuitive. In real life, GCF is used in situations that require even distribution, such as dividing a set of items into equal parts without leftovers. This slide will introduce the concept of GCF, explain its importance in simplifying fractions, and explore its practical applications. Encourage students to think of scenarios where they might need to use GCF, such as when sharing treats or organizing objects, to help them relate to the concept.

Methods to Find the Greatest Common Factor (GCF) – Prime factorization method – Break numbers into prime factors, then multiply common primes. – List out all factors method – Write down factors of each number, then find the largest common one. – Euclidean algorithm method – Use division to find GCF, more suitable for larger numbers. | This slide introduces three different methods for finding the Greatest Common Factor (GCF) of two or more numbers. The prime factorization method involves breaking down each number into its prime factors and then identifying the common factors to multiply together. The listing method is straightforward but can be time-consuming; it requires listing out all the factors of each number and finding the largest one that appears in both lists. The Euclidean algorithm is a more advanced technique that uses a series of divisions to efficiently find the GCF, especially useful for larger numbers. Encourage students to practice each method with examples and understand when each method is most appropriate to use.

Finding the Greatest Common Factor (GCF) – GCF via prime factorization – Break down 48 & 64 into prime factors, then identify common ones. – List factors to find GCF – Write all factors of 18 & 27, find the largest common factor. – Class practice: GCF of 42 & 56 – Use methods learned to calculate GCF for 42 & 56 together. | This slide is aimed at providing students with examples and practice on finding the Greatest Common Factor (GCF). Start by explaining prime factorization, a method where numbers are broken down into their prime number factors. Demonstrate this with 48 and 64, showing the breakdown and how to identify the common prime factors to find the GCF. Next, illustrate finding the GCF of 18 and 27 by listing out all the factors of each number and identifying the highest number that appears in both lists. For class practice, guide students to apply these methods to find the GCF of 42 and 56. Encourage students to work in pairs or groups to foster collaborative learning and ensure they understand the process before attempting it individually.

GCF in Fractions – Simplify fractions with GCF – Use GCF to reduce fractions to simplest form – Example: Simplify 36/48 – Find GCF of 36 and 48, then divide both by it – Practice: Simplify 20/45 – Find GCF of 20 and 45, then simplify | This slide introduces the concept of simplifying fractions by using the Greatest Common Factor (GCF). Start by explaining that the GCF is the largest number that divides two or more numbers without a remainder. Show how to find the GCF of the numerator and denominator and then divide both by this number to simplify the fraction. For the example, walk through the steps to find the GCF of 36 and 48, which is 12, and then divide both terms by 12 to simplify the fraction to 3/4. For the practice, guide students to find the GCF of 20 and 45, and simplify the fraction themselves. Encourage students to work through the problem and share their answers. This exercise will help reinforce their understanding of GCF and its application in simplifying fractions.

Class Activity: GCF Scavenger Hunt – Find numbered objects in class – Pair up for GCF discovery – Calculate the GCF together – Use division or prime factorization – Share GCF findings with class | This interactive activity is designed to help students apply their knowledge of the greatest common factor (GCF) in a fun and engaging way. Students will search the classroom for objects that have numbers on them, such as page numbers, rulers, or blocks. After pairing up, they will work together to find the GCF of the numbers they’ve found using methods like division or prime factorization. Once they’ve calculated the GCF, each pair will share their findings with the class, explaining how they arrived at their answers. This will not only reinforce their understanding of GCF but also encourage collaboration and communication skills. As a teacher, be prepared to offer guidance and support as needed and ensure that each pair has a chance to present their findings.

Wrapping Up: GCF and Next Steps – Recap: What is GCF? – Greatest Common Factor, largest number that divides two or more numbers. – GCF’s role in simplifying fractions – Helps reduce fractions to their simplest form. – Homework: Find GCF from scavenger hunt – Study for the upcoming GCF quiz – Review today’s lesson and practice with your scavenger hunt numbers. | As we conclude today’s lesson on the Greatest Common Factor (GCF), remind students of its definition and significance in mathematics, particularly in simplifying fractions. For homework, students should apply what they’ve learned to find the GCF of numbers they collected during a scavenger hunt activity. This practical application reinforces their understanding. Additionally, inform students that there will be a quiz on GCF in the next class to assess their comprehension. Encourage them to review their notes, complete their homework, and practice additional problems to prepare for the quiz. Offer support and resources for students who may need extra help.