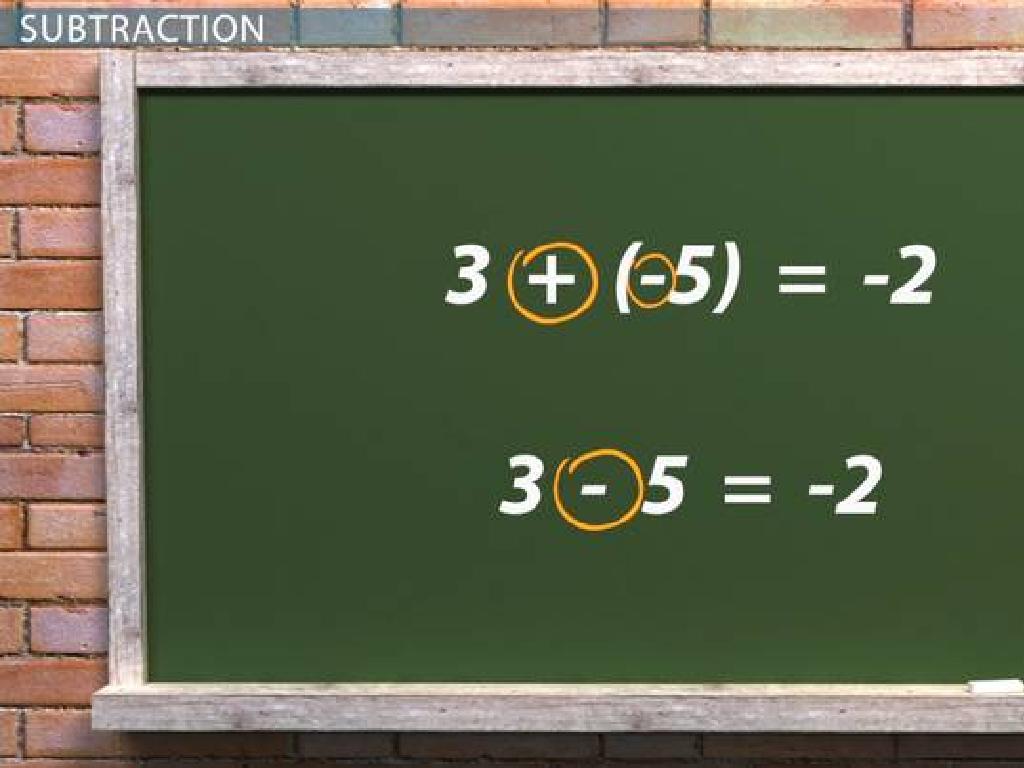Your next great Lessn starts here.

Introduction to One-Step Equations – Understanding One-Step Equations – Equations with one operation to solve – Definition of One-Step Equation – An equation needing only one mathematical step to isolate the variable – Real-life One-Step Equation Examples – Balancing a checkbook or making a recipe – Solving One-Step Equations – Use inverse operations to solve for the variable | This slide introduces the concept of one-step equations, which are the simplest form of algebraic equations and a foundational skill in mathematics. A one-step equation requires just one operation addition, subtraction, multiplication, or division to solve for the unknown variable. To give students a practical understanding, present real-life scenarios where they might encounter such equations, like balancing a checkbook (if you have $50 and write a check for $30, how much do you have left?) or adjusting a recipe (if a recipe calls for 2 eggs and you have 5, how many more do you need?). Emphasize the use of inverse operations to isolate the variable and solve the equation. Encourage students to practice with various examples to gain confidence in solving one-step equations.

Identifying Parts of an Equation – Variables: Letters representing numbers – Constants and Coefficients – Constants are fixed values; coefficients are numbers multiplied by variables – Equal sign: Balance in equations – It shows that what is on one side is equal to the other side – Practice with sample equations – Identify variables, constants, and coefficients in examples | This slide introduces students to the fundamental components of one-step equations. Variables are symbols, usually letters, that stand in for unknown numbers. Constants are specific numbers that remain the same, while coefficients are numbers that multiply the variables. The equal sign is a critical part of the equation, indicating that two expressions are equivalent. To solidify this understanding, students will identify these parts in sample equations, enhancing their ability to solve one-step equations. Encourage students to practice by writing down different parts of equations from their textbook or worksheets provided.

Solving Addition Equations – Understanding equation solutions – Solving means finding the value of the variable that makes the equation true. – Use inverse to find the variable – To isolate the variable, we do the opposite operation on both sides of the equation. – Example: x + 5 = 12 – In this equation, x is the unknown we are solving for. – Isolate x by subtracting 5 – Doing the inverse operation, we get x = 12 – 5, which simplifies to x = 7. | This slide introduces the concept of solving one-step addition equations by using inverse operations. Start by explaining what it means to solve an equation: finding the value of the variable that makes the equation true. Emphasize the use of inverse operations, in this case, subtraction, to isolate the variable on one side of the equation. The example provided should be worked through step-by-step, showing students how to subtract 5 from both sides to find that x equals 7. Encourage students to practice with similar equations and reinforce the idea that whatever operation is done to one side of the equation must also be done to the other side to maintain balance.

Solving Subtraction Equations – Use addition to isolate variable – Example: Solve x – 3 = 8 – Add 3 to both sides to get x = 11 – Check the solution’s validity – Substitute x with 11: 11 – 3 = 8 – Practice with similar problems – Try solving x – 5 = 10, x – 2 = 7 | This slide focuses on solving one-step subtraction equations by using the inverse operation, addition. Start by explaining that to isolate the variable, we add the same number to both sides of the equation that was subtracted from the variable. Use the example x – 3 = 8 to demonstrate this process step by step. After finding the value of x, it’s crucial to check the solution by substituting the variable with the obtained value to see if the equation holds true. Encourage students to practice with additional problems to reinforce the concept.

Solving Multiplication Equations – Divide to isolate the variable – Example: 4x = 20 – To find x, divide both sides by 4: x = 20 / 4 – Division as inverse of multiplication – Division undoes multiplication, helping solve for x – Practice with similar equations – Try solving 5x = 15 and 6x = 24 on your own | This slide introduces the concept of solving one-step multiplication equations by using division. Emphasize that division is the inverse operation of multiplication, which is key to isolating the variable. The example 4x = 20 is solved by dividing both sides of the equation by 4, resulting in x = 5. Encourage students to understand that whatever operation is done to one side of the equation must be done to the other to maintain balance. Provide additional practice problems for students to apply this concept independently, reinforcing their understanding of solving equations.

Solving Division Equations – Isolate variable by multiplying – Example: x/5 = 7 – Multiply both sides by 5 to find x – Use reciprocal operations – Reciprocal of division is multiplication – Solve x/5 = 7 by multiplying by 5 – x = 7 * 5, so x equals 35 | This slide introduces students to solving one-step division equations. The goal is to isolate the variable on one side of the equation. To do this, students should perform the reciprocal operation, which is multiplication in the case of division. For example, if x is divided by 5, students should multiply both sides of the equation by 5 to solve for x. This will cancel out the division by 5 on the left side, leaving x alone. It’s important to emphasize that whatever operation is done to one side of the equation must be done to the other to maintain balance. The example provided will help students see this process in action. Encourage students to practice with additional problems to reinforce the concept.

Solving One-Step Equations: Class Activity – Solve equations as a group – Student participation at the board – Invite different students to solve problems on the board – Discuss various solution methods – Compare subtraction, addition, multiplication, division approaches – Emphasize understanding over memorization – Reinforce the concept that understanding the process is key | This slide is designed for an interactive class activity focused on solving one-step equations. Encourage students to actively participate by coming up to the board to solve equations. This will help them gain confidence and provide an opportunity for peer learning. Discuss the different methods that can be used to solve one-step equations, such as adding, subtracting, multiplying, or dividing both sides of the equation to isolate the variable. Emphasize the importance of understanding the underlying principles rather than just memorizing procedures. Provide guidance and positive feedback to foster a supportive learning environment. Possible activities include solving equations with different operations, peer review of solutions, and creating their own one-step equations for classmates to solve.

Class Activity: Equation Race – Form teams for the race – Solve one-step equations – Each team works on different equations – First team to finish wins – Ensure correct solutions – Accuracy is just as important as speed | This activity is designed to encourage collaboration and to practice solving one-step equations in a fun, competitive setting. Divide the class into small teams, ensuring a mix of abilities in each group. Provide each team with a set of one-step equations that they must solve together. The first team to complete their set correctly wins the race. Emphasize the importance of accuracy over speed to avoid careless mistakes. Possible variations of the activity could include a relay race where each student solves one equation before passing it on, or a ‘sudden death’ round where teams go head-to-head with a single equation. This activity will help reinforce students’ understanding of one-step equations and improve their problem-solving skills.

Homework: Mastering One-Step Equations – Complete the assigned worksheet – Worksheet includes a mix of problems – Practice one-step equations at home – Reinforce today’s lesson with extra practice – Review solutions and methods – Check your work for accuracy – Next topic preview: Two-step equations – Get a head start on upcoming concepts | The homework assignment is crucial for reinforcing the concepts learned in class about solving one-step equations. The worksheet provided should cover a range of equation types to ensure students get comprehensive practice. Encourage students to dedicate time at home to work through the problems, reminding them of the importance of practice in mastering math skills. Additionally, advise them to review their methods and solutions to solidify their understanding. Looking ahead, give students a heads-up that the next topic will be two-step equations, which builds on the foundation they’re currently working on. This will help them understand the progression of concepts and prepare them for future lessons.