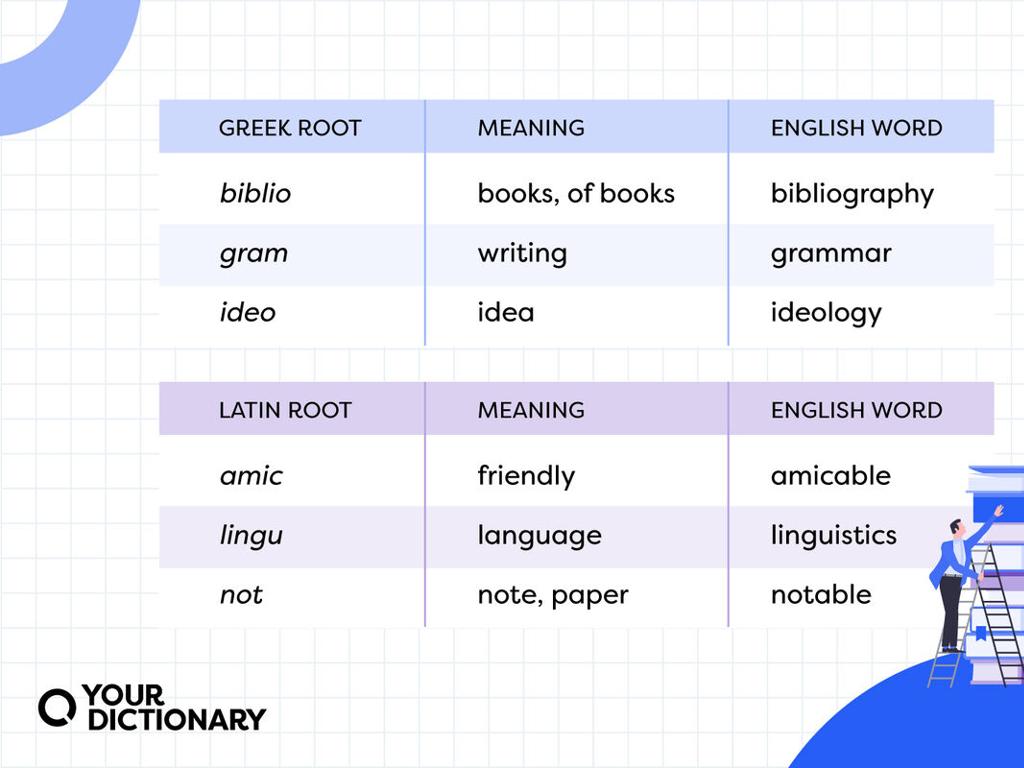
Identify Equivalent Equations
Subject: Math
Grade: Eighth grade
Topic: One-Variable Equations
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Identifying Equivalent Equations
– Understanding one-variable equations
– Equations with one variable represent a balance
– Defining what equations are
– An equation is a statement that two expressions are equal
– Identifying equivalent equations
– Equivalent equations have the same solution
– Exploring balance in equations
– Maintaining balance is key to equivalence
|
This slide introduces students to the concept of one-variable equations and sets the stage for understanding equivalent equations. Begin by explaining that an equation is like a balance scale, where both sides must be equal. Then, define an equation as a mathematical statement that asserts the equality of two expressions. Emphasize that equivalent equations, although they may look different, have the same solution. Use examples to show how different equations can represent the same relationship. For instance, 2x + 3 = 7 and 4x + 6 = 14 are equivalent because both have the solution x = 2. Encourage students to think of their own examples and to practice identifying equivalent equations. This foundational understanding will be crucial as they progress in algebra.
Understanding Equivalent Equations
– Define equivalent equations
– Equations with different appearances but identical solutions
– Examples of equivalent equations
– E.g., 2(x + 3) = 14 and x + 3 = 7 are equivalent
– Significance in mathematics
– They simplify complex problems & validate solutions
– Exploring equivalence
|
This slide introduces the concept of equivalent equations, which are fundamental in algebra. Equivalent equations may look different but share the same solution set. Provide simple examples to illustrate this, such as showing how multiplying both sides of an equation by the same number doesn’t change the solution. Emphasize the importance of understanding equivalent equations as they allow students to simplify complex problems, check their work, and understand different forms of the same mathematical relationship. Encourage students to practice creating equivalent equations by applying algebraic operations such as addition, subtraction, multiplication, and division to both sides of an equation.
Properties of Equality: Crafting Equivalent Equations
– Review addition/subtraction properties
– If a = b, then a + c = b + c, and a – c = b – c
– Review multiplication/division properties
– If a = b, then a * c = b * c, and a / c = b / c
– Apply properties for equivalent equations
– Use properties to form equations with the same solutions
– Practice with example equations
– Example: If 3x + 4 = 19, then 3x = 15 is equivalent
|
This slide aims to consolidate students’ understanding of the properties of equality and how they can be applied to create equivalent equations. Begin by reviewing the addition and subtraction properties, emphasizing that adding or subtracting the same number from both sides of an equation preserves equality. Similarly, review the multiplication and division properties, highlighting that multiplying or dividing both sides of an equation by the same nonzero number also maintains equality. Then, demonstrate how to apply these properties to form new equations that have the same solutions as the original. Provide practice problems for students to try, such as transforming 3x + 4 = 19 into 3x = 15 by subtracting 4 from both sides, to reinforce the concept. Encourage students to explain their reasoning and to check their work by solving both the original and the equivalent equation.
Identifying Equivalent Equations
– Determining equation equivalence
– Two equations are equivalent if they have the same solutions.
– Substitution to verify equivalence
– Replace variables with numbers to see if both equations give the same result.
– Practice with equivalent equations
– Solve sample problems to apply the concept of equivalence.
– Strategies for checking equivalence
|
This slide introduces the concept of equivalent equations in one-variable algebraic expressions. Start by explaining that equivalent equations have the same solutions, meaning they intersect at the same points on a graph. Teach students how to use substitution as a method to verify if two equations are equivalent by replacing the variable with a number and checking if both sides of the equation remain equal. Provide practice problems for students to apply this knowledge and reinforce learning. Discuss different strategies students can use to check for equivalence, such as simplifying expressions or graphing. Encourage students to explain their reasoning during practice to deepen their understanding.
Solving One-Variable Equations
– Step-by-step equation solving
– Isolate the variable using inverse operations
– Finding satisfying solutions
– Solutions must work in both original and equivalent equations
– Example: Equivalent equations
– Solve 2x + 3 = 7 and x + 6 = 10 to find x
– Verifying solutions
– Check by plugging x back into the equations
|
This slide introduces students to the process of solving one-variable equations and understanding the concept of equivalent equations. Start by explaining the step-by-step method to isolate the variable, emphasizing the use of inverse operations such as addition, subtraction, multiplication, and division. Highlight the importance of finding solutions that satisfy both the original and the equivalent equations. Provide an example by solving two equations that have the same solution, such as 2x + 3 = 7 and x + 6 = 10, and demonstrate how to verify that the solution is correct by substituting the value of x back into both equations. Encourage students to practice with additional examples and verify their solutions to reinforce their understanding.
Class Activity: Equivalent Equations Challenge
– Group activity: Match equivalent equations
– Work in teams to find pairs of equivalent equations
– Individual task: Craft your own equations
– Use variables and constants to form equations
– Share findings: Present to the class
– Explain your reasoning behind each equation
– Discuss: Understand different solutions
– Listen to others and explore various approaches
|
This interactive class activity is designed to deepen students’ understanding of equivalent equations. Begin with a group activity where students collaborate to match different but equivalent equations. Then, have each student create their own set of equivalent equations, encouraging creativity and application of concepts learned. Afterward, students will present their equations to the class, explaining their thought process. This will be followed by a class discussion to explore the different methods used to create equivalent equations. As a teacher, facilitate the discussion, ensuring that each student understands the principles of forming equivalent equations. Provide guidance and feedback during the activities, and consider offering several examples to help students get started.
Wrapping Up: Equivalent Equations
– Review of equivalent equations
– Homework: Worksheet completion
– Find and solve equivalent equations in the worksheet.
– Next topic: One-variable inequalities
– We’ll explore how inequalities differ from equations.
– Keep practicing equation skills
|
As we conclude today’s lesson on identifying equivalent equations, ensure students have grasped the concept of equations that have the same solutions. For homework, assign a worksheet that requires them to practice finding and solving equivalent equations, reinforcing today’s learning. Looking ahead, inform students that the next class will delve into inequalities within one-variable equations, which will build on their understanding of equivalency. Encourage them to keep practicing their equation-solving skills, as this will be crucial for mastering upcoming topics. Provide a brief session at the end for any questions students may have about the lesson or homework.