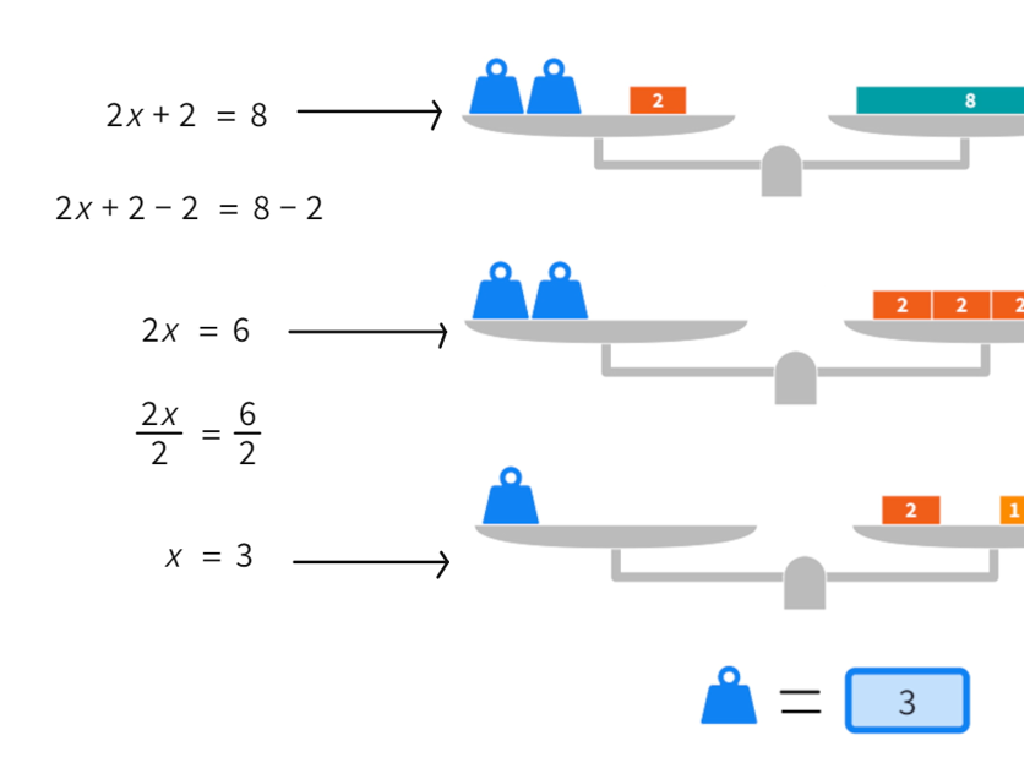
Solve Two-Step Equations: Complete The Solution
Subject: Math
Grade: Eighth grade
Topic: One-Variable Equations
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Introduction to Two-Step Equations
– Define one-variable equations
– Equations with one unknown variable, e.g., x + 5 = 12
– Introduce two-step equations
– Equations needing two operations to solve, e.g., 2x + 3 = 7
– Real-life two-step equation examples
– Budgeting allowance, cooking recipes
– Solving two-step equations
– Isolate the variable: subtract/add, then divide/multiply
|
Begin with a review of one-variable equations to ensure students have a solid foundation. Introduce two-step equations as an extension of what they already know, emphasizing that two operations are needed to find the solution. Provide relatable examples such as managing a budget or following a recipe, which naturally involve two-step processes. Demonstrate solving two-step equations step by step, starting with addition or subtraction to move one term to the other side of the equation, followed by division or multiplication to solve for the variable. Encourage students to practice with various examples and to check their solutions by substituting the value back into the original equation.
Solving Two-Step Equations
– Define two-step equations
– Equations requiring two operations to solve, e.g., 2x + 3 = 11
– Understand constants, variables, coefficients
– Constants are fixed numbers, variables are unknowns, and coefficients are numbers multiplied by variables
– Recognize two-step equation structure
– Equations like ax + b = c, where two operations are needed: one to remove b and one to isolate x
– Practice identifying two-step equations
|
This slide introduces students to the concept of two-step equations, which are equations that require two inverse operations to solve for the variable. Start by defining the components: constants (fixed values), variables (unknowns we aim to solve for), and coefficients (numbers multiplying the variable). Show how these components form a two-step equation and guide students to identify such equations. Provide examples like 2x + 3 = 11 and explain the steps to solve: subtract 3 from both sides, then divide by 2. Encourage students to practice with similar equations and to recognize the structure of two-step equations in various forms.
Solving Two-Step Equations: Step 1
– Isolate the variable term
– Use addition or subtraction to get the variable term alone
– Example: 3x + 4 = 19
– Subtract 4 from both sides: 3x = 15
– Work through the example
– Divide both sides by 3: x = 5
– Try a practice problem
|
This slide introduces the first step in solving two-step equations: isolating the variable. Start by explaining the importance of getting the variable on one side of the equation. Use an example like 3x + 4 = 19 to demonstrate the process. Subtract 4 from both sides to get 3x = 15, then divide both sides by 3 to find x = 5. After the example, provide a similar problem for the students to solve on their own, ensuring they understand the concept. As they work, circulate the room to offer help and check for understanding. This practice solidifies the skill of isolating the variable, preparing them for the next step of solving two-step equations.
Solving Two-Step Equations: Step 2
– Isolate variable: multiply/divide
– If equation is 2x + 3 = 11, divide both sides by 2 to find x
– Work through a class example
– Example: Solve 3x – 5 = 16 together
– Individual practice problem
– Solve 4x + 7 = 19 on your own
|
This slide focuses on the second step of solving two-step equations, which involves isolating the variable. Start by explaining that after dealing with addition or subtraction, the next step is to multiply or divide to get the variable alone. Use an example like 2x + 3 = 11 and show the process of dividing both sides by 2 to solve for x. Then, work through another example as a class to reinforce the concept. Provide a practice problem for students to solve individually, such as 4x + 7 = 19, and encourage them to apply the same steps. This will help solidify their understanding of isolating the variable in two-step equations. Be prepared to assist students who may need extra help and offer praise to those who solve it correctly.
Checking Your Solution in Two-Step Equations
– Importance of verifying solutions
Ensures the solution is correct and understanding is clear.
– Substituting solutions into equations
Replace the variable with your solution and see if the equation balances.
– Class practice on solution checking
Use examples solved earlier to practice checking.
– Reinforce accurate problem-solving
|
This slide emphasizes the significance of checking the solutions to two-step equations. It’s crucial for students to understand that finding an answer isn’t the end; verifying it ensures accuracy and solidifies their comprehension of the concepts. Demonstrate how to substitute the solution back into the original equation to check if both sides are equal, reinforcing the idea that equations are balanced systems. During class practice, encourage students to apply this method to examples they’ve previously solved, fostering a habit of meticulousness and precision in their approach to solving equations. This will not only help them in math but also instill a valuable skill for problem-solving in general.
Avoiding Common Mistakes in Two-Step Equations
– Consistency on both sides
– Always perform the same mathematical operation on each side of the equation.
– Adhere to order of operations
– Remember PEMDAS: Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.
– Verify each step
– After each operation, check to ensure the equation remains balanced.
– Practice with examples
– Regular practice with varied problems helps reinforce correct methods.
|
When solving two-step equations, it’s crucial to maintain balance by performing the same operations on both sides of the equation. This slide addresses common errors such as neglecting to apply changes to both sides and confusing the order of operations, which can lead to incorrect solutions. Emphasize the importance of the mnemonic PEMDAS to remember the correct sequence of operations. Encourage students to double-check their work at each step to catch mistakes early. Provide a variety of practice problems in class and as homework to help students become proficient in solving two-step equations without making these common mistakes.
Class Activity: Equation Relay Race
– Split class into teams
– Solve part of the equation
– Each member solves a step in the two-step equation
– Pass it to the next teammate
– Ensure smooth transition between team members
– First team to finish wins
|
This activity is designed to encourage collaboration and to reinforce the concept of solving two-step equations. Divide the class into small groups, and give each team a different two-step equation to solve. One student from each team will solve the first step and then pass the equation to the next team member to solve the second step. The first team to solve the equation correctly wins. Make sure to prepare several equations so that each team has one to work on. Possible variations of the activity could include timed rounds, complex equations for bonus points, or a ‘relay’ where students must run to a designated spot to pass on their solution. This will help students to engage with the material actively and to practice their problem-solving skills in a fun and competitive environment.
Homework: Mastering Two-Step Equations
– Solve assigned homework problems
– Create your own two-step equations
Craft equations and solve them to enhance understanding
– Utilize available help resources
Access online tools, textbooks, and ask for teacher assistance
– Review and practice regularly
|
This slide aims to reinforce the students’ understanding of solving two-step equations by providing them with structured homework and practice opportunities. Assign a set of problems that cover a range of difficulties to ensure thorough practice. Encourage creativity by having students come up with their own equations, which can be shared with classmates for additional practice. Remind them of the support available, including online resources, textbooks, and the opportunity to seek help from teachers during office hours. Emphasize the importance of regular review to solidify their skills in solving two-step equations. For the next class, prepare to discuss common challenges faced in the homework to address any widespread issues.