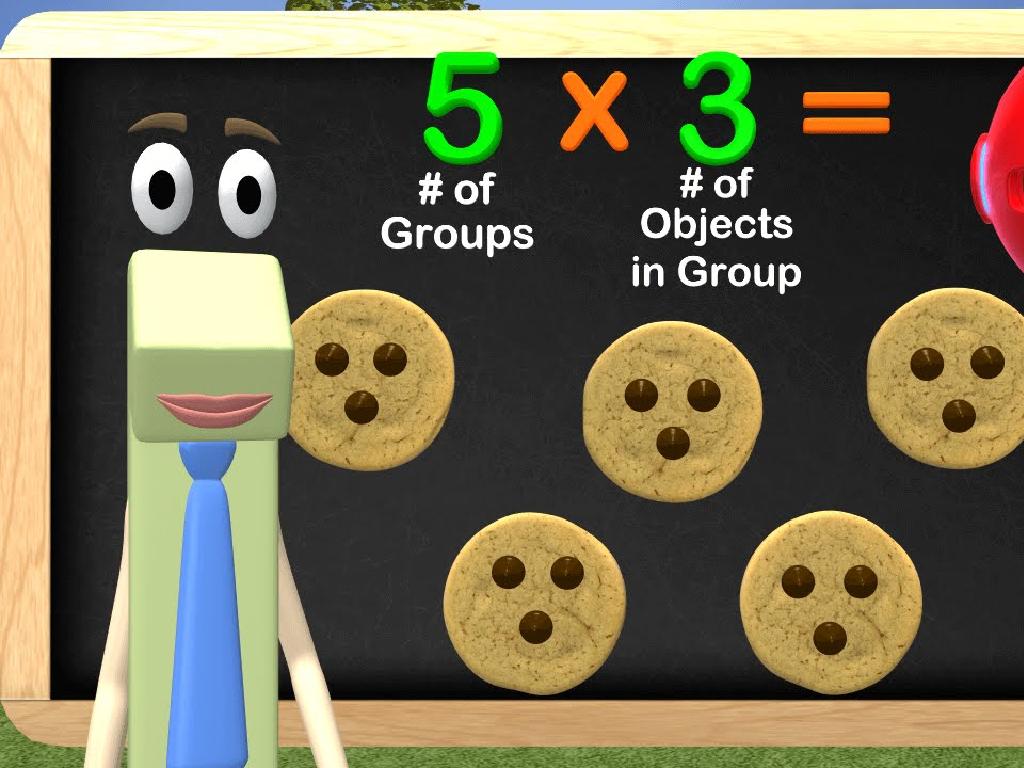Your next great Lessn starts here.

Introduction to One-Variable Equations – Understanding basic equations – Equations are like scales, they must balance – Defining one-variable equations – An equation with only one unknown value, e.g., x + 3 = 7 – Real-life one-variable examples – Budgeting allowance, or measuring ingredients – Solving equations with diagrams – Use diagrams to visualize and solve equations | Begin the lesson by explaining that equations are like balances; both sides must be equal. Introduce one-variable equations as equations that contain only one unknown variable that we are solving for. Provide real-life examples where one-variable equations are applicable, such as budgeting a weekly allowance or measuring ingredients for a recipe. Emphasize the importance of understanding the concept of variables in everyday life. Finally, demonstrate how diagrams can be used to represent and solve equations, making abstract concepts more concrete. Encourage students to draw diagrams for given equations and practice solving them.

Equations Representing Real Situations – Convert words to expressions – Translate verbal descriptions into algebraic expressions – Find variables in situations – Variables represent unknowns in problems, like ‘number of apples’ – Write equations for scenarios – Use variables to form equations that depict real-life situations – Solve the created equations – Apply math operations to find the value of the variables | This slide aims to teach students how to translate real-world situations into mathematical equations. Start by showing how to turn descriptive words into mathematical expressions, identifying what the variables represent in the context of the problem. Then, guide students through writing equations that correspond to these situations. Emphasize the importance of understanding what the variable stands for and how to choose the correct mathematical operations to represent the scenario. Finally, demonstrate solving these equations to find the value of the unknown variable. Provide examples such as calculating total cost from unit price and quantity, or finding the total number of items when given parts of a whole. Encourage students to practice with various examples to gain confidence.

Diagrams and Equations in Math – Diagrams as visual equations – Visual tools like diagrams can represent equations and their solutions. – Number lines and scales example – For instance, a number line shows the value of numbers, and a balancing scale can represent equality. – Create diagrams from equations – Given an equation, draw a diagram that illustrates it, such as using a balance for 3 + x = 7. – Practice with real-world problems | This slide introduces students to the concept of representing equations through diagrams, which is a crucial skill for visualizing and solving mathematical problems. Start by explaining how diagrams serve as another form of expressing equations. Use a number line to show positive and negative values, and a balancing scale to demonstrate the concept of equality in equations. Then, guide students to convert a written equation into a diagram, reinforcing their understanding of the equation’s components. Finally, provide practice problems that involve real-world scenarios where students can apply this skill, such as determining the number of items needed to balance weights or using a number line to find a missing value.

Solving One-Variable Equations – Understanding equation goals – The goal is to find the value of the unknown variable that makes the equation true. – Using inverse operations – Inverse operations reverse effects of arithmetic operations to help solve equations. – Isolating the variable – Move the variable to one side of the equation to find its value. – Checking the solution – Substitute the variable’s value back into the original equation to verify its correctness. | This slide introduces the process of solving one-variable equations, which is a fundamental skill in algebra. Start by explaining the goal of solving an equation: to find the value of the variable that makes the equation true. Discuss inverse operations such as addition/subtraction and multiplication/division, and how they are used to isolate the variable on one side of the equation. Emphasize the importance of checking the solution by substituting the variable’s value back into the original equation to ensure it satisfies the equation. Provide examples of simple one-variable equations and demonstrate the step-by-step process of solving them. Encourage students to practice with different equations and check their solutions.

Class Activity: Equation Creation – Create your own equations – Work in groups on equations – Represent real-life problems with equations – Solve the equations together – Use diagrams to visualize and solve – Share solutions with the class – Discuss different methods used | This activity is designed to encourage collaborative learning and to deepen students’ understanding of one-variable equations. Students will work in small groups to create their own equations based on diagrams provided. They will then solve these equations, using the diagrams to aid their understanding. After solving, each group will share their solutions and the methods they used with the class, allowing for discussion of different approaches. For the teacher: Prepare diagrams that can be translated into equations, ensure each group has a different diagram to promote a variety of solutions during the sharing session. Possible activities: 1) Balancing scales diagrams, 2) Objects with price tags to create budget equations, 3) Distance markers to create travel-related equations, 4) Mixing colors or ingredients in recipes to form ratio equations.

Wrapping Up: Equations & Diagrams – Review today’s key points – Homework: 5 equation problems – Solve equations that match diagrams – Emphasize consistent practice – Regular practice improves skills – Encourage questions next class | As we conclude today’s lesson on writing and solving one-variable equations from diagrams, it’s important to recap the main concepts to reinforce learning. For homework, students are assigned five problems to solve, which will help them apply what they’ve learned in a practical context. Remind students that mastering math skills requires consistent practice, and encourage them to approach these problems with a positive mindset. Let them know that questions are welcome in the next class, as discussing challenges can lead to a deeper understanding of the material.