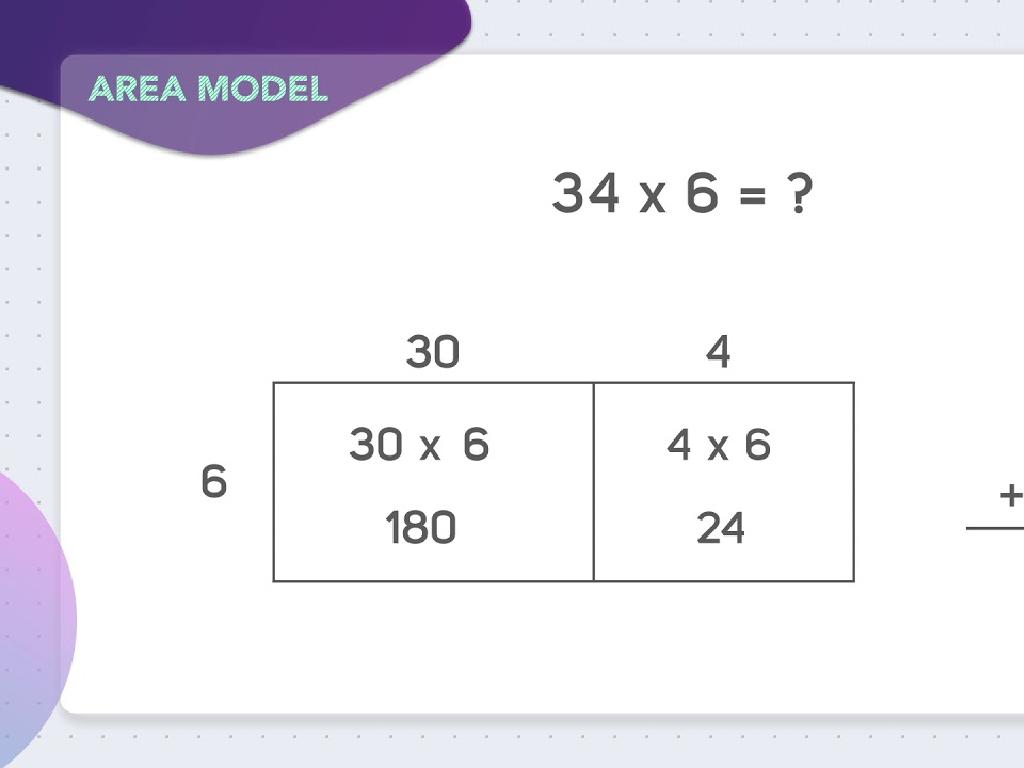
Divide Mixed Numbers
Subject: Math
Grade: Seventh grade
Topic: Operations With Fractions
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Dividing Mixed Numbers
– Understanding mixed numbers
– A mix of whole numbers and fractions, like 2 1/3
– Importance of division in fractions
– Helps solve real-world problems, like splitting a recipe
– Converting mixed numbers to improper fractions
– Multiply the whole number by the denominator, add the numerator
– Dividing improper fractions
– Invert the divisor and multiply to find the quotient
|
Today’s lesson introduces students to dividing mixed numbers, a key skill in understanding and operating with fractions. Begin by explaining what mixed numbers are and how they combine whole numbers with fractions. Emphasize the real-life applications of dividing mixed numbers, such as adjusting recipes or dividing quantities into smaller parts. Teach students to convert mixed numbers into improper fractions, which simplifies the division process. Then, demonstrate how to divide these improper fractions by inverting the divisor and multiplying. Provide examples and practice problems to ensure students grasp the concept. Encourage questions and interactive participation to facilitate learning.
Review: Fractions & Mixed Numbers
– Recap of fraction basics
– Understanding mixed numbers
– A whole number combined with a fraction, e.g., 1 3/4
– Mixed vs. improper fractions
– Improper fractions have a numerator larger than the denominator, e.g., 7/4
– Converting between forms
– Learn to change mixed numbers to improper fractions and vice versa
|
Begin with a brief review of fractions, ensuring students recall that a fraction represents a part of a whole. Then, introduce mixed numbers as a combination of a whole number and a fraction, providing clear examples such as 1 3/4. Highlight the difference between mixed numbers and improper fractions, where the latter has a numerator greater than the denominator, like 7/4. Teach students the methods for converting between mixed numbers and improper fractions, as this skill is crucial for performing operations like division on mixed numbers. Provide practice problems for conversion and ensure to clarify any misconceptions about these foundational concepts.
Dividing Mixed Numbers: Conversion Step
– Why convert to improper fractions?
It simplifies division of mixed numbers.
– Steps for conversion
Multiply whole number by denominator, add numerator, place over original denominator.
– Class conversion practice
Let’s practice converting together!
– Understanding the importance
|
When dividing mixed numbers, it’s essential to convert them to improper fractions first to simplify the process. Start by explaining the rationale behind this conversion, emphasizing that it makes division more straightforward. Walk through the conversion steps: multiply the whole number by the denominator, add the numerator, and write this sum over the original denominator. Engage the class with practice problems, asking students to convert mixed numbers to improper fractions on their own, then review as a class. Highlight the importance of mastering this step before moving on to division, as it lays the groundwork for understanding more complex fraction operations.
Dividing Improper Fractions
– Recap: Keep-Change-Flip method
– Review how to divide fractions: Keep the first fraction, Change the division sign to multiplication, Flip the second fraction (reciprocal).
– Divide numerators and denominators
– After applying Keep-Change-Flip, divide the top numbers (numerators) and bottom numbers (denominators) separately.
– Examples of improper fraction division
– Let’s divide 7/4 by 2/3: Keep 7/4, Change to multiplication, Flip 2/3 to 3/2. Now multiply 7/4 by 3/2.
|
Begin the lesson by reviewing the Keep-Change-Flip method as a strategy to divide fractions, which is a foundational skill for dividing improper fractions. Emphasize the importance of understanding this method before moving on to more complex examples. Provide step-by-step guidance on how to divide the numerators and denominators separately after applying the Keep-Change-Flip method. Use clear examples of improper fractions to illustrate the process, such as dividing 7/4 by 2/3, and show how to simplify the result if necessary. Encourage students to practice with additional examples and to check their understanding by simplifying their answers.
Converting Improper Fractions to Mixed Numbers
– Convert result to mixed number
– Divide numerator by denominator
E.g., 17 divided by 5 is 3 with a remainder of 2
– Remainder becomes the fraction
Place the remainder over the original denominator, e.g., 2/5
– Combine whole number and fraction
The mixed number is 3 2/5
|
After dividing mixed numbers, students may get an improper fraction as a result. It’s crucial to teach them how to convert this back into a mixed number for ease of understanding and use in real-life situations. Start by dividing the numerator by the denominator to find the whole number part of the mixed number. The remainder of this division becomes the numerator of the fractional part, which is then placed over the original denominator. Combining these two parts gives the final mixed number. For example, if the result is 17/5, dividing 17 by 5 gives 3 with a remainder of 2, resulting in the mixed number 3 2/5. Practice with several examples to ensure understanding.
Dividing Mixed Numbers: A Step-by-Step Guide
– Convert mixed to improper fractions
– Example: 3 1/2 becomes 7/2
– Change division to multiplication
– Keep the first, multiply by the reciprocal of the second
– Multiply fractions and simplify
– After multiplication, reduce the fraction to its simplest form
– Convert to mixed number if needed
– If the numerator is larger than the denominator, convert it
|
Begin by explaining the necessity of converting mixed numbers to improper fractions to simplify the division process. Emphasize the importance of understanding the reciprocal and how division of fractions can be turned into multiplication. Provide examples for each step, such as converting 3 1/2 to 7/2, then multiplying by the reciprocal of another fraction. After the multiplication, guide students on how to simplify fractions by finding the greatest common divisor. Lastly, demonstrate how to convert an improper fraction back to a mixed number, ensuring students can interpret the final result. Encourage practice with various examples and provide additional problems for homework.
Dividing Mixed Numbers: Practice Session
– Class walkthrough of practice problems
– Individual attempts by students
– Review solutions collectively
– Discuss the steps taken to solve the problems
– Highlight common errors to avoid
– For example, not converting mixed numbers to improper fractions
|
This slide is designed for a collaborative classroom practice session on dividing mixed numbers. Begin by solving a few problems as a class to demonstrate the process. Then, allow students to work on problems individually to apply what they’ve learned. Afterward, come together as a class to discuss the solutions. Emphasize the importance of converting mixed numbers to improper fractions before dividing and remind students to multiply by the reciprocal of the divisor. Discuss common mistakes such as forgetting to simplify the answer or not converting back to a mixed number if needed. Provide a variety of problems with different levels of difficulty to cater to all students. Encourage students to ask questions and share their thought processes.
Class Activity – Divide and Conquer!
– Pair up and solve mixed number divisions
– Present a problem and solution to the class
– Reinforce division concepts
– Encourage learning from peers
|
In this interactive class activity, students will work in pairs to tackle division problems involving mixed numbers, which will help solidify their understanding of the concept. Each pair will be responsible for solving a set of problems and then presenting one of those problems, along with their solution, to the rest of the class. This exercise is designed not only to reinforce the mathematical technique of dividing mixed numbers but also to foster a collaborative learning environment where students can learn from each other. As a teacher, prepare a diverse set of problems of varying difficulty to accommodate different skill levels. Encourage students to explain their thought process during the presentation to enhance their peers’ comprehension. Possible activities for different pairs could include creating word problems, solving provided equations, or even developing a short teaching segment to explain their problem to the class.
Wrapping Up: Dividing Mixed Numbers
– Summarize division steps
– Convert to improper fractions, multiply by the reciprocal, simplify if needed.
– Emphasize practice importance
– Regular practice solidifies understanding and improves speed.
– Homework assignment
– Complete set problems to reinforce today’s lesson.
|
As we conclude today’s lesson on dividing mixed numbers, it’s crucial to reiterate the steps for the students. Start by converting mixed numbers to improper fractions, then multiply by the reciprocal of the divisor, and finally, simplify the result if possible. Emphasize to the students that mastering division of mixed numbers, like any other mathematical skill, requires regular practice. Assign a variety of problems as homework to ensure they apply what they’ve learned and become comfortable with the process. The homework should cover a range of difficulties to challenge all students and solidify their understanding.