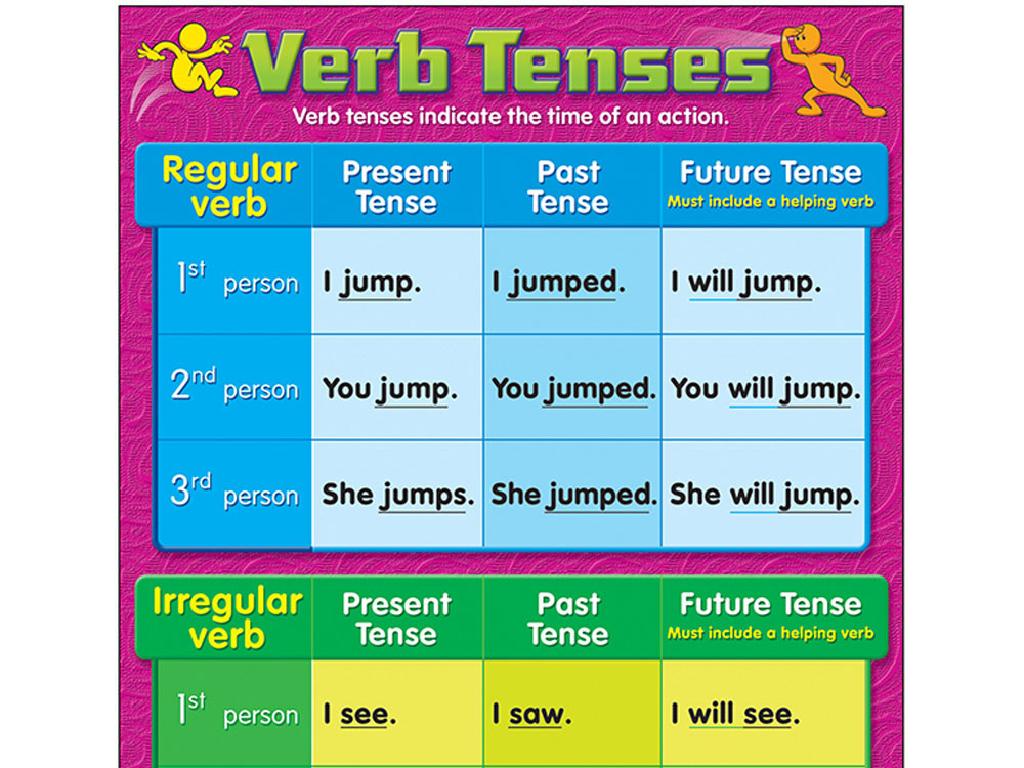
Multiply Mixed Numbers
Subject: Math
Grade: Seventh grade
Topic: Operations With Fractions
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Multiplying Mixed Numbers
– What are mixed numbers?
– A mix of whole numbers and fractions, like 2 1/3
– Steps to multiply mixed numbers
– Convert to improper fractions, multiply, simplify
– Real-world application
– Used in cooking, construction, and budgeting
– Practice problems
– Solve 2 1/3 x 1 1/2 as a class activity
|
Begin the lesson by explaining what mixed numbers are and how they differ from improper fractions. Emphasize the importance of being able to multiply mixed numbers in various real-world scenarios, such as doubling a recipe or calculating material lengths in construction. Walk through the steps of converting mixed numbers to improper fractions, performing the multiplication, and then simplifying the result. Provide several practice problems for the students to solve, ensuring they understand each step of the process. Encourage students to ask questions and work together on the class activity to reinforce their learning.
Review: Fractions & Mixed Numbers
– Recap: What are fractions?
– Fractions represent parts of a whole.
– Understanding mixed numbers
– Mixed numbers combine whole numbers and fractions.
– Real-life mixed number examples
– Recipes, measuring lengths, or time tracking.
– Practice with mixed numbers
|
Begin with a quick review of fractions, ensuring students recall that fractions represent a part of a whole, with a numerator and denominator. Then, introduce mixed numbers as a combination of a whole number and a fraction, which are often used in everyday life. Provide relatable examples such as cooking measurements (1 1/2 cups of sugar) or measuring lengths (2 3/4 inches of ribbon). Encourage students to think of other examples where they encounter mixed numbers. Conclude with practice problems to solidify their understanding of how to identify and work with mixed numbers.
Converting Mixed Numbers to Improper Fractions
– Why convert to improper fractions?
It simplifies multiplication of mixed numbers.
– The conversion formula
(Whole number × Denominator) + Numerator = Improper Fraction
– Step-by-step conversion
Example: Convert 3 2/5 to an improper fraction.
– Class practice activity
Let’s practice converting with examples together!
|
This slide introduces the concept of converting mixed numbers to improper fractions, which is a crucial step in multiplying mixed numbers. Start by explaining the necessity of this conversion for simplifying the multiplication process. Then, present the formula for conversion and go through a step-by-step example, such as converting 3 2/5 to an improper fraction by multiplying 3 (the whole number) by 5 (the denominator), then adding 2 (the numerator), resulting in 17/5. Engage the class with practice problems, ensuring to provide a variety of examples. Encourage students to work in pairs or groups to foster collaborative learning and to discuss the conversion process. As a teacher, circulate the room to offer guidance and address any misconceptions.
Multiplying Mixed Numbers
– Review simple fraction multiplication
Recall multiplying fractions like 1/2 x 3/4
– Multiply numerators and denominators
For 2/3 x 4/5, multiply 2 x 4 and 3 x 5
– Simplify the product
Reduce the fraction 8/15 to its simplest form
– Practice with mixed numbers
Convert mixed numbers to improper fractions to multiply
|
Begin with a quick review of multiplying simple fractions to ensure students recall the process. Emphasize that when multiplying fractions, we multiply the numerators together and the denominators together. After obtaining the product, it’s important to simplify the fraction by finding the greatest common divisor and dividing both numerator and denominator by it. For mixed numbers, guide students to first convert them to improper fractions before multiplying. Provide examples and practice problems for students to apply these steps, such as 1 1/2 x 2 2/3, and encourage them to simplify their answers fully.
Multiplying Improper Fractions
– Convert mixed numbers to improper fractions
– Multiply numerators together and denominators together
– Apply multiplication to improper fractions
– Example: 7/4 x 3/2 = (7×3)/(4×2)
– Solve sample problems as a class
– Use a step-by-step approach to ensure understanding
– Strategies for managing large numbers
– Break down large numbers into smaller parts
|
This slide focuses on the multiplication of improper fractions, a key skill in understanding operations with fractions. Start by converting any mixed numbers into improper fractions. Emphasize the multiplication process: multiplying the numerators together to get the new numerator, and the denominators together for the new denominator. Work through sample problems as a class to demonstrate the process and to allow students to practice. Discuss strategies for keeping track of large numbers, such as breaking them down into smaller parts or using estimation to check the reasonableness of answers. Encourage students to ask questions and provide assistance as needed to ensure mastery of the concept.
Multiplying Mixed Numbers
– Convert mixed numbers to improper fractions
– Multiply the whole number by the denominator, add the numerator
– Multiply the improper fractions together
– Use cross-cancellation for efficiency before multiplying
– Convert the product to a mixed number
– Divide the numerator by the denominator of the product
– Simplify the result if necessary
– Reduce fractions to simplest form for final answer
|
This slide introduces the process of multiplying mixed numbers, which is a key skill in understanding operations with fractions. Start by converting mixed numbers to improper fractions, ensuring students understand the reason behind this step. Emphasize the importance of cross-cancellation before multiplying to simplify calculations. After obtaining the product, guide students through converting it back to a mixed number, which involves dividing the numerator by the denominator and using the remainder as the new numerator. Finally, remind students to always simplify their answer. Provide examples and practice problems to reinforce the concept.
Multiplying Mixed Numbers: Practice Session
– Class solves problems together
– Individual practice for students
– Try problems on your own to test understanding
– Share solutions and discuss
– Explain your solution to the class
– Understand different methods
– Learn various strategies to solve problems
|
This slide is designed to facilitate a practice session on multiplying mixed numbers. Begin with a collaborative problem-solving session where a problem is solved as a class to model the process. Then, assign individual practice problems for students to work on their own, ensuring they apply the concepts learned. Afterward, have students share their solutions and the methods they used with the class, fostering a collaborative learning environment. Encourage students to explain their reasoning and be open to learning different approaches from their peers. This will help them see the diversity in problem-solving strategies and reinforce their understanding of the topic.
Real-World Application: Multiplying Mixed Numbers
– Multiplication in daily life
– Recipe adjustments with fractions
– Doubling a recipe: 1 1/2 cups sugar becomes 3 cups
– Discuss real-life examples
– Group activity: Share experiences where you used fractions
– Understand practical relevance
– Relate math skills to everyday tasks to see their value
|
This slide aims to show students how the math they learn in class applies to everyday situations, particularly in tasks like cooking. For instance, when a recipe calls for 1 1/2 cups of an ingredient and you want to double the recipe, you need to multiply the mixed number by 2, resulting in 3 cups. Encourage students to think of and discuss other scenarios where they might need to multiply mixed numbers, such as in construction (measuring materials) or in sewing (calculating fabric lengths). This discussion will help them see the value of understanding how to work with fractions and mixed numbers beyond the classroom. Provide guidance on how to approach multiplying mixed numbers and facilitate the group discussion to ensure all students participate and contribute.
Class Activity: Recipe Challenge
– Work in groups to adjust a recipe
– Double the recipe using mixed numbers
– If original calls for 1 1/2 cups, double is 3 cups
– Present your new recipe to the class
– Explain the multiplication process
– Describe steps taken to multiply each ingredient amount
|
This interactive class activity is designed to help students apply their knowledge of multiplying mixed numbers in a practical context. Divide the class into small groups and provide each with a simple recipe. Instruct them to calculate the new measurements for each ingredient to double the recipe. This will require converting mixed numbers to improper fractions, multiplying, and then converting back to mixed numbers. Afterward, each group will present their adjusted recipe and explain the mathematical process they used. Encourage clear communication of each step and the importance of precision in measurements. Possible variations for different groups could include tripling a recipe or scaling it down by half. This activity will reinforce their understanding of operations with fractions in a fun, real-world application.
Wrapping Up: Multiplying Mixed Numbers
– Review of multiplying mixed numbers
– Remember to convert to improper fractions
– Practice makes perfect
– Consistent practice improves skills
– Homework: 10 practice problems
– Solve and show work for each problem
– Bring questions to next class
– Ready to help with any challenges
|
As we conclude today’s lesson on multiplying mixed numbers, it’s crucial to emphasize the importance of practice in mastering this concept. Remind students that converting mixed numbers to improper fractions is a key step in the multiplication process. For homework, assign 10 problems that vary in difficulty to ensure a comprehensive understanding. Encourage students to attempt all problems and to show their work for each step. Let them know that they should bring any questions or difficulties they encounter to the next class, where we will address them and provide further clarification. This will not only reinforce today’s lesson but also prepare them for more complex operations with fractions.