Your next great Lessn starts here.

Adding Integers: Understanding the Basics – What are integers? – Integers include positive, negative numbers, and zero. – Rules for adding integers – Same signs add and keep, different signs subtract. – Why integers matter – Integers are key in math concepts like finance, science. – Examples of integer addition – E.g., -3 + 7 = 4; -6 + (-4) = -10. | This slide introduces the concept of integers and the rules for adding them, which is a foundational skill in mathematics. Integers are the set of whole numbers and their opposites, crucial for understanding real-world scenarios such as temperature changes, financial transactions, and scientific measurements. Emphasize the rules for adding integers with like signs (add the absolute values and keep the sign) and with unlike signs (subtract the smaller absolute value from the larger one and take the sign of the larger absolute value). Provide clear examples to illustrate these rules. Encourage students to think of situations where they might need to add integers in their daily lives.

Understanding Integers in Math – Define integers – Integers include whole numbers and their negatives, excluding fractions and decimals. – Positive vs. Negative numbers – Positive numbers are above zero, negative numbers are below zero. – Real-life integer examples – Temperatures, bank balances, and elevations can be expressed using integers. – Adding integers – When adding integers, same signs sum up, opposite signs subtract. | Integers are the set of whole numbers and their opposites. They do not include fractions or decimals. It’s crucial for students to differentiate between positive and negative numbers, as this understanding is fundamental to operations with integers. Provide real-life scenarios where integers are used, such as temperatures (above/below zero), bank account balances (deposits/withdrawals), or elevations (above/below sea level). When adding integers, reinforce the rule that adding two positives or two negatives simply combines their values, while adding a positive and a negative number requires finding the difference between the two values. Use number lines and real-life situations to practice adding integers.

Rules for Adding Integers – Adding same sign integers – Sum the values and keep their common sign. – Adding different sign integers – Find the difference and use the sign of the larger absolute value. – Subtract and keep larger number’s sign – Using a number line for addition – Visualize addition by moving along the number line. | When teaching students to add integers, start by explaining that the process differs depending on the signs of the numbers involved. If the integers have the same sign, simply add their absolute values and keep the common sign. For integers with different signs, subtract the smaller absolute value from the larger one, and keep the sign of the integer with the larger absolute value. Emphasize that the absolute value is the distance from zero, not the sign. Introduce the number line as a tool to help visualize the process, where students can physically move in the positive or negative direction to find the sum. Provide examples and practice problems to reinforce these concepts.

Adding Integers with Same Sign – Adding same sign integers – Example: +4 + +3 = +7 – When signs match, just add the numbers – Use a number line for visualization – A number line helps to see the addition – Practice: +7 + +2 – Try it yourself to reinforce the concept | This slide introduces students to the concept of adding integers with the same sign. Start by explaining that when two positive numbers are added, the result is also positive. Use the concrete example of +4 + +3 to show that you simply add the numbers and keep the positive sign. Introduce a number line as a visual aid to help students understand how adding positive numbers moves to the right on the line. Provide the practice problem of +7 + +2 and ask students to solve it, reinforcing the concept that adding two integers with the same sign is straightforward. Encourage students to visualize the problem on a number line and to check their work with peers.

Adding Integers with Different Signs – Understand adding opposite signs – Example: +6 + (-9) – Starting at +6, move 9 steps left to end at -3 – Use a number line for visualization – A number line helps to see the movement from positive to negative – Practice: -5 + (+8) – Start at -5, move 8 steps right to end at +3 | This slide introduces students to the concept of adding integers with different signs. Begin by explaining that when adding a positive and a negative number, we are essentially subtracting the smaller number from the larger one. Use the concrete example of +6 + (-9) to illustrate this, showing that we start at +6 on the number line and move 9 steps to the left, landing on -3. Emphasize the importance of direction on the number line: moving left for negative and right for positive. For the practice problem, guide students to apply the same principle: starting at -5 and moving 8 steps to the right, ending at +3. Encourage students to solve more problems like these to become comfortable with the concept.

Let’s Practice Together: Adding Integers – Pair up and solve integer additions – Example 1: Calculate -7 + +4 – Combining a negative and a positive integer – Example 2: Calculate +3 + -5 – Combining a positive and a negative integer – Discuss solutions with the class | This class activity is designed to reinforce the concept of adding integers with different signs. Students will pair up to work collaboratively, which will help them learn from each other and discuss different approaches to solving the problems. Example 1 involves adding a negative integer to a positive one, while Example 2 involves adding a positive integer to a negative one. After solving, pairs will discuss their solutions and methods with the class, providing an opportunity for peer learning. As a teacher, circulate around the room to offer guidance and ensure that students understand the rules for adding integers. Possible variations for different pairs could include using larger numbers, adding more than two integers, or including zero in the mix.

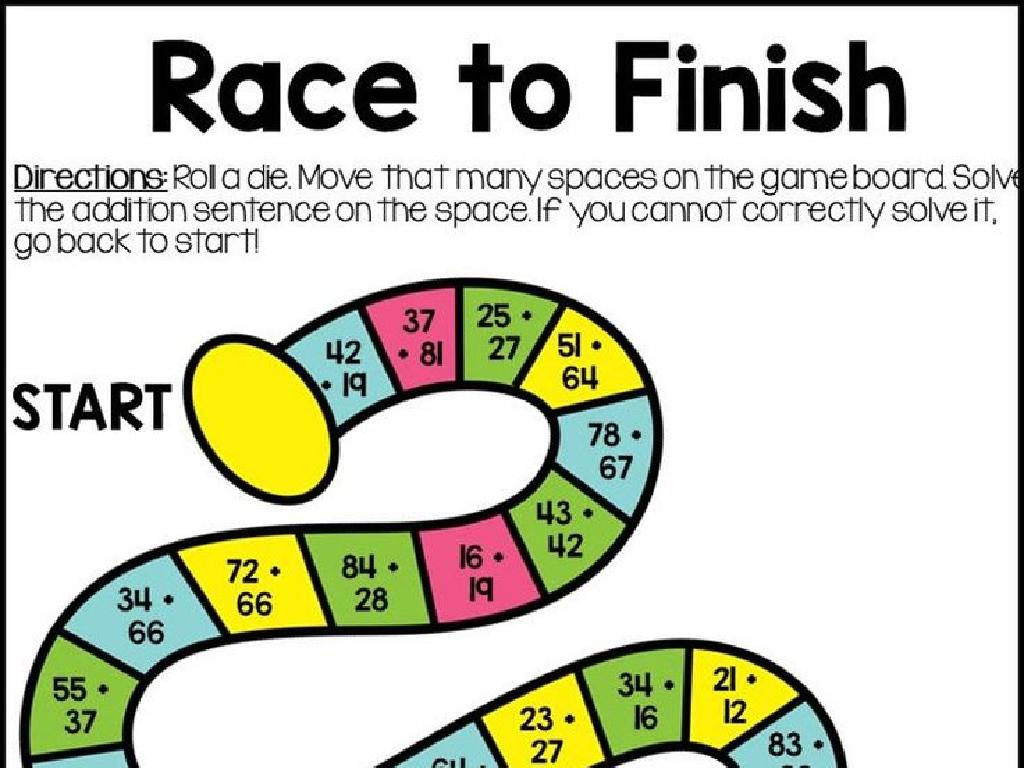
Class Activity: Integer Addition Race – Split into teams for the race – Solve integer addition problems – Add integers to find the sum, e.g., -3 + 7 = 4 – Each correct answer advances your team – Race to finish first and win! | This activity is designed to encourage teamwork and practice with adding integers in a fun, competitive setting. Divide the class into small groups, ensuring a mix of abilities in each team. Provide each team with a set of integer addition problems. As they solve each problem correctly, they move a marker forward on a game track drawn on the board or provided on paper. The first team to reach the finish line wins. Consider having different difficulty levels for the problems to cater to varying skill levels within the class. Possible variations of the activity could include a relay race format, a point system for extra challenging questions, or a ‘lifeline’ where teams can ask for a hint but must sacrifice some progress.

Conclusion & Practice: Adding Integers – Recap: Rules for adding integers – Summarize today’s integer addition rules. – Practice makes perfect – Regular practice is key to mastering math skills. – Homework: Integer addition worksheet – Complete the provided worksheet to practice. – Be prepared to review answers – We’ll go over the worksheet in the next class. | As we wrap up today’s lesson on adding integers, it’s crucial to emphasize the importance of practice in mastering mathematical concepts. The homework assignment is a worksheet that reinforces today’s lesson and prepares students for more complex problems. Encourage students to attempt all problems and assure them that we will review the answers together in the next class, providing an opportunity to clarify any doubts. Remind them that making mistakes is a part of the learning process, and the goal is to learn from those mistakes.