Rational Numbers: Find The Sign
Subject: Math
Grade: Seventh grade
Topic: Operations With Rational Numbers
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Welcome to Rational Numbers
– Define rational numbers
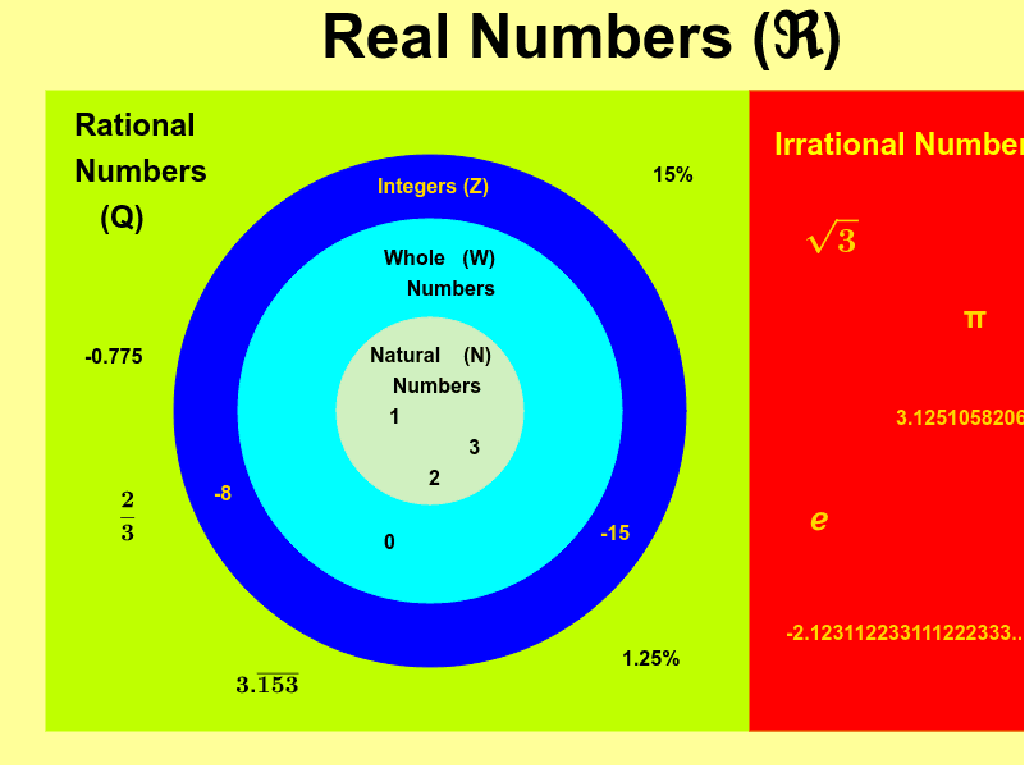
– A number that can be expressed as a fraction a/b, where a and b are integers, and b is not zero.
– Characteristics of rational numbers
– They include integers, fractions, and terminating or repeating decimals.
– Identifying rational numbers
– Determine if numbers like 1/2, -3, 0.75, or 5/0 are rational.
– Real-world examples
– Money, measurements, and time often involve rational numbers.
|
This slide introduces the concept of rational numbers, which are any numbers that can be expressed as the quotient or fraction of two integers. The denominator cannot be zero because division by zero is undefined. Rational numbers encompass a broad range of numbers including positive and negative integers, fractions, and decimals that terminate or repeat. Provide examples such as 1/2, -3, and 0.75 to illustrate rational numbers and ask students to identify whether given numbers are rational. Use relatable examples like money (e.g., $0.50), measurements (e.g., 3/4 cup), and time (e.g., half an hour) to show rational numbers in real-world contexts. Encourage students to think of other examples and explain why they are rational numbers.
Identifying Rational Numbers
– Rational vs. Irrational Numbers
– Rational numbers can be written as a fraction, irrational cannot.
– Steps to Identify Rational Numbers
– Determine if a number can be expressed as a fraction.
– Practice with examples
– Use examples like 1/2, 0.75, and 2 to illustrate.
– Class activity: Find the Sign
|
This slide introduces students to the concept of rational numbers as part of the broader topic of operations with rational numbers. Begin by explaining the difference between rational and irrational numbers, emphasizing that rational numbers can be expressed as a fraction of two integers, while irrational numbers cannot. Provide a step-by-step guide on how to identify rational numbers, and use clear examples to help students understand. Include practice problems that involve identifying rational numbers from a set of various numbers. Conclude with a class activity where students ‘find the sign’ of given rational numbers, determining whether they are positive or negative based on the numerator and denominator. This activity will reinforce their understanding of rational numbers and prepare them for operations involving these numbers.
Operations with Rational Numbers: Finding the Sign
– Adding/subtracting rational numbers
– Multiplying/dividing rational numbers
– Rules for determining the sign
– Same signs result in a positive, different signs result in a negative
– Practice with examples
– Example: (-3/4) x (2/3) = -1/2, (-3/4) + (3/4) = 0
|
This slide focuses on understanding how to find the sign of the result when performing operations with rational numbers. When adding or subtracting, if the numbers have the same sign, the result keeps that sign. If they have different signs, subtract the smaller absolute value from the larger and keep the sign of the larger. For multiplication and division, if both numbers have the same sign, the result is positive; if the signs are different, the result is negative. Provide students with various examples to practice these rules and solidify their understanding. Encourage them to predict the sign before calculating the exact answer.
Determining the Sign in Rational Numbers
– Multiplying two positives
– When you multiply two positive numbers, the result is always positive.
– Multiplying positive and negative
– A positive times a negative number gives a negative result.
– Multiplying two negatives
– The product of two negative numbers is positive.
– Division follows multiplication rules
– The sign for division is determined the same way as in multiplication.
|
This slide is aimed at helping students understand the rules for finding the sign of a result when performing operations with rational numbers. Rule 1 states that the product of two positive numbers is positive. Rule 2 indicates that when a positive number is multiplied by a negative, the result is negative. Rule 3 reveals that multiplying two negative numbers results in a positive product. Lastly, Rule 4 teaches that the rules for determining the sign in division are the same as those for multiplication. It’s crucial for students to memorize these rules as they form the foundation for working with rational numbers. Provide examples for each rule to ensure students can apply them in different scenarios.
Finding the Sign in Rational Numbers
– Multiplying a positive by a negative
– Results in a negative number, e.g., 3 × -4 = -12
– Dividing a negative by a positive
– Results in a negative number, e.g., -15 ÷ 5 = -3
– Multiplying two negatives
– Results in a positive number, e.g., -2 × -2 = 4
|
This slide aims to help students understand how to determine the sign of the result when performing operations with rational numbers. Start by explaining that the sign of the answer depends on the signs of the numbers involved in the operation. Use the examples provided to illustrate the rules: multiplying a positive number by a negative always gives a negative result, dividing a negative by a positive also yields a negative result, and multiplying two negative numbers results in a positive number. Encourage students to remember these rules as they will be fundamental in solving more complex problems involving rational numbers. Provide additional examples and practice problems to reinforce the concept.
Practice Problems: Finding the Sign
– Solve Practice Problem 1
– Determine the sign of the product or quotient
– Solve Practice Problem 2
– Apply rules for multiplying/dividing rational numbers
– Solve Practice Problem 3
– Use the rules to find the sign of the result
– Discuss solutions and strategies
– Share problem-solving techniques and learn from peers
|
This slide is designed to engage students in active practice with finding the sign of the result when multiplying or dividing rational numbers. Each practice problem should involve different combinations of positive and negative rational numbers to illustrate the rules for determining the sign. Encourage students to explain their reasoning for each step. After solving, discuss as a class to reinforce the concept that the product or quotient of two rational numbers with the same sign is positive, while if they have different signs, the result is negative. This will help solidify their understanding and prepare them for more complex operations with rational numbers.
Class Activity: Sign Scavenger Hunt
– Find pairs of rational numbers
– Determine product or quotient sign
– Is the result positive or negative?
– Share results with the class
– Discuss how you found the sign
|
This interactive class activity is designed to help students understand the rules for determining the sign of a product or quotient of rational numbers. Students will work in pairs or small groups to find pairs of rational numbers, either from provided examples or by creating their own. They will then calculate the products or quotients and determine if the result is positive or negative. Encourage students to consider the rules for multiplying and dividing positive and negative numbers. After the activity, students will share their results and discuss the strategies they used to determine the signs. Possible variations of the activity could include using number cards, a worksheet with pre-written number pairs, or a digital tool that generates rational numbers for students to work with.
Wrapping Up: Signs in Rational Numbers
– Recap of sign rules in operations
– Why signs matter in math
– Correct signs are crucial for accurate results in math problems.
– Homework: Practice worksheet
– Complete the worksheet on finding the sign with rational numbers.
– Be prepared to discuss answers
– We’ll review the worksheet in the next class, so try your best!
|
Today’s lesson focused on understanding how to determine the sign of an answer when performing operations with rational numbers. Emphasize the importance of this skill, as it is fundamental to solving math problems correctly. For homework, students are assigned a worksheet that provides practice on this topic, which will help reinforce their learning. Encourage students to attempt all problems and remind them that we will go over the worksheet in the next class, discussing any challenges they faced. This will not only help them understand the material better but also prepare them for more complex math concepts in the future.