Your next great Lessn starts here.

Introduction to Percents – Understanding Percents – A percent represents a part of a whole divided into 100 equal parts. – Percents in daily life – Used in sales tax, discounts, and statistics. – Percents, fractions, and decimals – 50% is 1/2 and 0.50 in decimal form. – Estimating percents | Begin the lesson by explaining that a percent is a way of expressing a number as a fraction of 100. It’s a concept that students will encounter frequently in real life, such as in calculating tips at restaurants, determining sales discounts, or understanding interest rates. Make sure to illustrate the direct relationship between percents, fractions, and decimals, showing how they can be converted into one another. For example, 25% is the same as 1/4 and 0.25. Emphasize the importance of estimating percents to quickly assess situations in everyday life, such as approximating the amount of a discounted item without a calculator. Provide examples and practice problems to solidify their understanding.

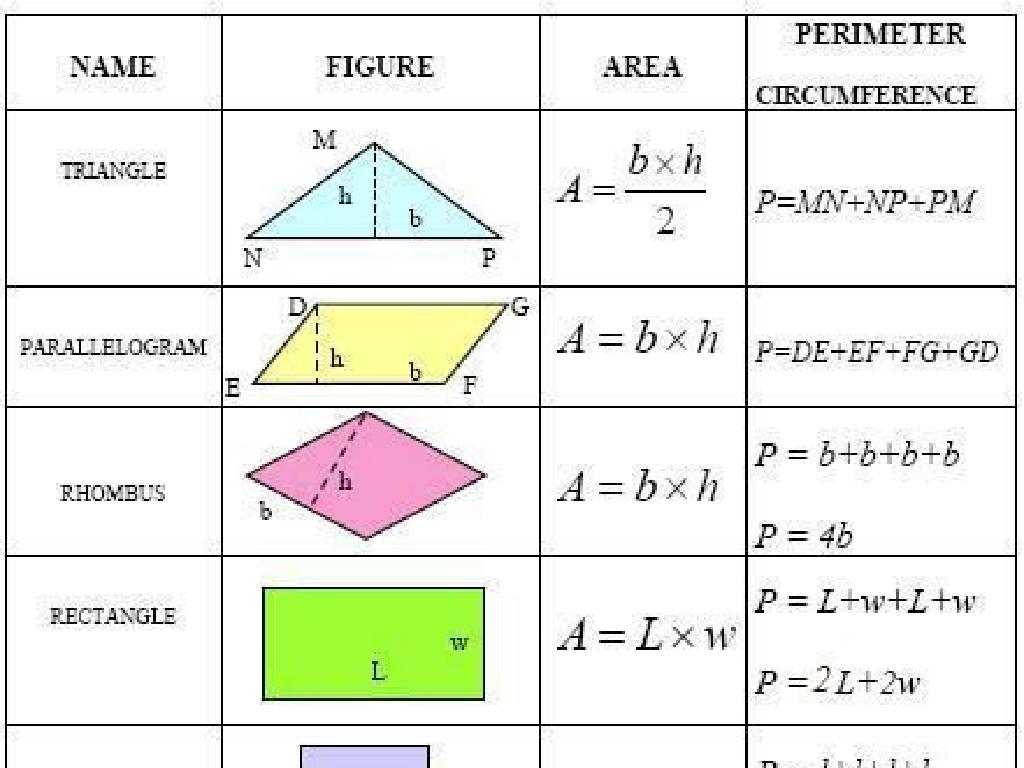
Understanding Percents – Percent means ‘per hundred’ – Visual examples: 1%, 50%, 100% – 1% as 1 square shaded in a 100-square grid, 50% as half shaded, 100% fully shaded – Convert fractions to percents – To convert a fraction to a percent, divide the top number by the bottom number, then multiply by 100 – Convert decimals to percents – To convert a decimal to a percent, multiply by 100 and add a percent sign | Begin with the basic definition of percent as a part out of 100. Use visual aids to show what 1%, 50%, and 100% look like on a grid to give students a clear and tangible understanding of these concepts. Then, explain the process of converting fractions and decimals to percents by providing examples and working through them step by step. For instance, converting 1/2 to a percent involves dividing 1 by 2 to get 0.5 and then multiplying by 100 to get 50%. Similarly, to convert 0.75 to a percent, multiply by 100 to get 75%. Encourage students to practice with different fractions and decimals to solidify their understanding.

Estimating Percents – Importance of estimating percents – Rounding numbers for estimation – Round to nearest whole number to simplify calculations – Using 25%, 50%, 75% benchmarks – Common percents to gauge others against – Practice estimation with examples – Estimate 20% tip on a $50 bill or find 70% of 100 | Understanding how to estimate percents is crucial for making quick, practical decisions in everyday life, such as calculating tips or discounts. Teach students to round numbers to the nearest whole number to simplify the process of finding percents. Introduce benchmarks of 25%, 50%, and 75% as reference points to help estimate other percents more easily. Provide examples such as estimating a 20% tip on a $50 bill or finding what is 70% of 100. Encourage students to practice with different scenarios to become comfortable with estimation. This skill will aid them in mental math and in situations where exact numbers are not necessary.

Estimating Percents of Numbers – Steps to estimate percents – Identify the percent, convert it to a fraction or decimal, and multiply by the number – Example: 10%, 20%, 30% of a number – For 10% of 50, think 10/100 * 50 = 5. Similarly, calculate 20% and 30% – Use estimation to verify answers – After calculating, use estimation to check if the answer seems reasonable – Practice estimation with exercises | This slide introduces the concept of estimating percents as a useful tool for quickly calculating the approximate value of a percentage of a number. Begin by explaining the steps to convert a percent into a more manageable form (fraction or decimal) and then multiply by the number to estimate the percent of that number. Provide clear examples using common percents like 10%, 20%, and 30% to solidify understanding. Emphasize the importance of estimation in checking work for reasonableness, which can help students catch mistakes in their calculations. Encourage practice with a variety of exercises to build confidence and proficiency in estimating percents.

Estimating Percents of Numbers – Estimate 25% of 60 – About 1/4 of 60 is close to 15 – Estimate 70% of 150 – 70% is like 7/10 of 150, roughly 105 | This slide presents two practice problems to help students learn to estimate percents of numbers. For the first problem, guide students to understand that 25% is the same as 1/4, so they can divide the number 60 by 4 to estimate the answer. For the second problem, explain that 70% is the same as 7/10, which means they can find 10% of 150 first by dividing by 10, and then multiply by 7 to estimate the answer. Encourage students to round numbers when necessary to make the estimation easier. These examples will help solidify their understanding of percents as parts of 100 and how to use this knowledge to estimate quickly and accurately.

Estimating Percents in Real Life – Estimation in shopping discounts – Approximate how much you save during sales, e.g., 20% off a $50 item is about $10 off. – Calculating tips at restaurants – A quick way to estimate a 15% tip is to find 10% of the bill and add half of that amount again. – Figuring out sales tax – Use estimation to quickly calculate the tax added to your purchases. | Understanding how to estimate percents is a valuable skill in everyday life. When shopping, estimation can help students quickly determine how much they can save during sales. For example, if a student sees a 20% discount on a $50 item, they should be able to estimate that they’ll save around $10. Similarly, when dining out, estimating a 15% tip can be done by first finding 10% of the total bill and then adding half of that amount again. Lastly, being able to estimate the sales tax on purchases allows students to better manage their money and understand the final cost of items. Encourage students to practice these skills by looking at real prices and bills to apply what they’ve learned.

Class Activity: Percent Estimation Game – Form pairs or small groups – Receive a set of scenarios – Estimate percents in scenarios – Use mental math to approximate percents – Explain reasoning behind estimates – Justify your answers with logical thinking | This interactive class activity is designed to enhance students’ understanding of estimating percents through practical application. Divide the class into pairs or small groups to foster collaboration. Provide each group with a set of real-world scenarios that require them to estimate percents, such as finding the discount on a sale item or calculating the tip at a restaurant. Encourage students to use mental math strategies for estimation and to discuss their reasoning within their groups. As a teacher, circulate the room to guide discussions, clarify misconceptions, and challenge students with additional scenarios if needed. After the activity, bring the class together for a group discussion to share different estimation strategies and reasoning. This will help students learn from each other and recognize multiple methods for estimating percents.

Estimating Percents: Conclusion and Recap – Recap: Why estimate percents? – Estimating percents is crucial for quick calculations in shopping, statistics, and more. – Review: Estimation techniques – Rounding numbers and using benchmark percents like 50%, 25%, and 10% to estimate. – Homework: Practice makes perfect – Complete assigned problems to reinforce today’s lesson. – Keep practicing with real-life examples – Apply estimation skills to calculate discounts, tax, and tips. | As we conclude today’s lesson, remind students of the practical applications of estimating percents in daily life, such as calculating tips at a restaurant or discounts while shopping. Review the key techniques we’ve covered, emphasizing the use of benchmark percents and rounding for quick mental calculations. Assign homework problems that reinforce these concepts and encourage students to practice further. Remind them that proficiency comes with practice, and applying these skills to real-world scenarios will help solidify their understanding.