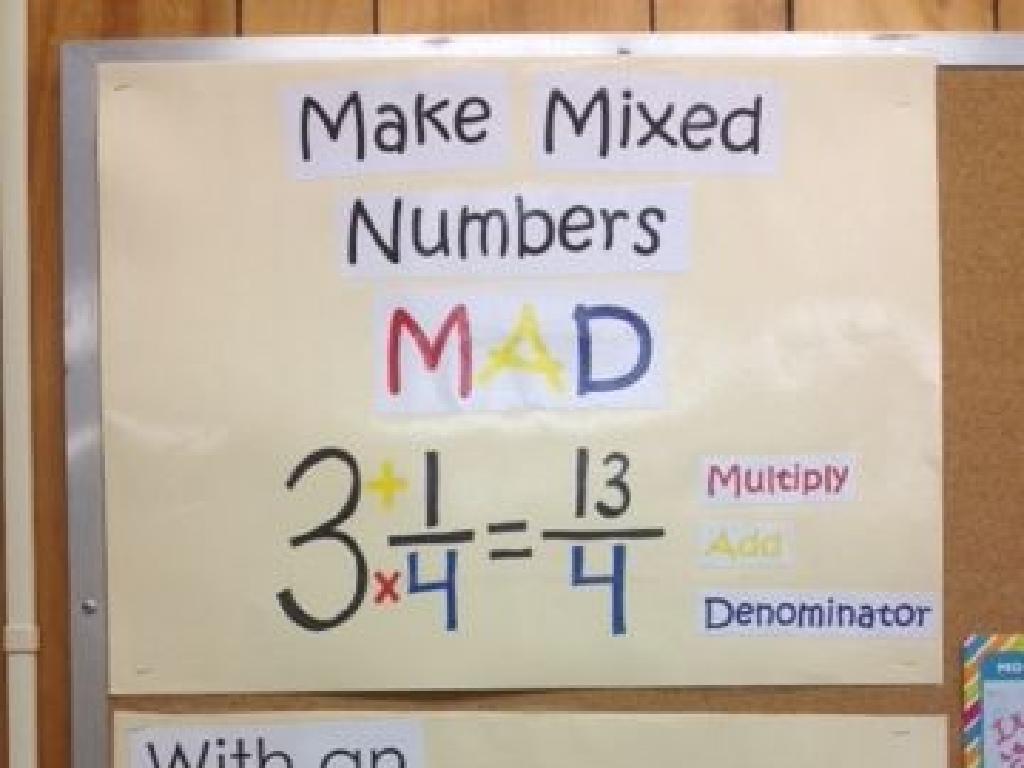Your next great Lessn starts here.

Introduction to Percent Equations – Understanding percents – Percents represent a part of a whole as fractions of 100 – Real-life percent applications – Used in discounts, interest rates, and statistics – Review: What is a percent? – A percent is a ratio that compares a number to 100 – Solving percent equations | This slide introduces the concept of percent equations to seventh-grade students. Begin by explaining that percents are a way to express fractions of 100, making it easier to understand parts of a whole. Illustrate with examples like a 25% discount on a $100 item means saving $25. Review the basic definition of a percent as a ratio, which is foundational knowledge before tackling percent equations. Emphasize the importance of percent equations in various real-life scenarios such as calculating sales tax, determining interest on savings, or analyzing data. The goal is to ensure students are comfortable with the concept of percents before moving on to solve percent equations.

Understanding Percent Equations – Define percent equation – An equation that represents the part as a percent of the whole. – Relation: part, whole, and percent – If a part is 25% of a whole, then 25% is the percent, the part is 25, and the whole is 100. – Everyday examples of percent equations – Finding discounts during sales, calculating tips at restaurants, or determining tax on purchases. | This slide introduces the concept of percent equations to students, explaining that a percent equation is a mathematical way to express a part as a fraction of a whole, with the fraction multiplied by 100 to get a percentage. It’s crucial to illustrate the relationship between the part, whole, and percent, ensuring students understand that the whole is always considered 100%. Provide relatable examples such as calculating a 20% discount on a $50 jacket, which involves finding what 20% of $50 is, to solidify their understanding. Encourage students to think of other scenarios where they might use percent equations in their daily lives.

Converting Percents, Fractions, and Decimals – Convert percents to fractions – To convert, divide the percent by 100 and simplify – Convert fractions to decimals – Multiply the decimal by 100 and add a percent sign – Convert decimals to percents – Divide the top by the bottom of the fraction, then multiply by 100 – Step-by-step practice problems – Work through examples together for clear understanding | This slide introduces the concept of converting between percents, fractions, and decimals, which is a fundamental skill in understanding percentages. Start by explaining the conversion process for each type, ensuring to highlight the importance of dividing or multiplying by 100. Provide clear examples for each conversion type. The practice problems should be designed to reinforce these concepts, with step-by-step solutions to guide students through the process. Encourage students to solve the problems on their own first, then review the solutions as a class. This will help them to solidify their understanding and give them the confidence to tackle similar problems independently.

Writing Percent Equations – Structure of percent equations – An equation of the form part = percent × whole – Translating word problems – Identify the ‘whole’, ‘part’, and ‘percent’ in the problem – Class practice activity – Use given word problems to form percent equations – Steps to write equations – 1) Read carefully 2) Identify elements 3) Translate to equation | This slide introduces students to the concept of percent equations, which are mathematical expressions that represent the relationship between a part, a whole, and a percentage. Start by explaining the structure of a percent equation, emphasizing that it involves finding a part of a whole based on a given percentage. Then, demonstrate how to translate a word problem into a percent equation by identifying keywords and values that represent the ‘whole’, ‘part’, and ‘percent’. During the class practice, provide students with a variety of word problems and guide them through the process of writing their own percent equations. Encourage them to follow the steps: read the problem carefully, identify the elements involved, and translate these into a mathematical equation. This activity will help solidify their understanding and prepare them for solving percent equations.

Solving Percent Equations – Steps to solve percent problems – Identify the base, rate, and percentage. Write the equation. – Using proportions to solve – Set up a proportion where % over 100 equals part over whole. – Interactive class example – We’ll solve ‘What is 30% of 150?’ as a class. – Practice solving together | This slide introduces the process of solving percent equations, a key concept in understanding percents. Start by explaining the three components of percent problems: the base (the whole amount), the rate (the percent), and the percentage (the part). Demonstrate how to translate a word problem into a percent equation and then into a proportion. Use an interactive example, such as finding 30% of 150, to engage the class and walk through the solution step by step. Encourage students to participate by asking questions and solving the problem on the board. After the example, facilitate a practice session where students work on similar problems in pairs or groups to reinforce their understanding.

Practice Problems: Solving Percent Equations – Solve individual percent equations – Pair up and exchange problems – Work with a partner, compare different approaches – Discuss solving strategies in groups – Share your strategy and understand others’ – Reflect on different methods used – Think about which strategy was most effective and why | This slide is designed to facilitate active learning through practice and collaboration. Students will begin by solving percent equations individually to build their confidence. They will then pair up to exchange problems with a classmate, which encourages peer learning and exposes them to different problem-solving methods. Following this, the class will engage in a group discussion to share their strategies and learn from each other. This collaborative approach not only reinforces their understanding of percent equations but also promotes critical thinking as they reflect on the effectiveness of various methods. The teacher should circulate during activities, provide guidance, and ensure that each student is both challenged and supported.

Avoiding Common Mistakes in Percent Equations – Misinterpreting the percent sign – Remember, 50% is the same as 0.5 or 50/100 – Incorrectly setting up the equation – Ensure the correct relationship between the parts and the whole – Forgetting to convert percentages – Always convert the percent to a decimal or fraction – Checking work for accuracy – Use the inverse operation to confirm the solution is correct | This slide aims to highlight frequent errors students make when solving percent equations and how to avoid them. Emphasize the importance of understanding the percent sign and its equivalence to decimals and fractions. Stress the need for careful equation setup, reflecting the problem’s context. Remind students to convert percentages to avoid calculation mistakes. Finally, teach them to check their answers by reversing the operation. For example, if they find 30% of a number, they can divide the result by 0.3 to check if it gives the original number. Encourage practice with different types of percent problems to build confidence and accuracy.

Class Activity: Percent Equation Scavenger Hunt – Understand scavenger hunt rules – Find hidden percent equations – Equations are placed in various locations – Solve the percent equations – Use knowledge of percents to find solutions – Discuss solutions as a class – Share different solving methods and answers | This interactive class activity is designed to engage students in solving percent equations through a scavenger hunt. Before starting, explain the rules: equations are hidden around the classroom, and students must locate and solve them. Provide a worksheet for students to record equations and their solutions. After the hunt, reconvene as a class to discuss the findings. Encourage students to explain their solving process and compare answers. This will help them learn from each other and clarify any misunderstandings. Possible variations of the activity could include working in pairs, timing the hunt, or offering small rewards for correct solutions.

Wrapping Up: Percent Equations – Review of percent equation solving – Homework: Percent practice worksheet Complete the worksheet to reinforce today’s lesson. – Find real-life percent applications Look for discounts, tax rates, or interest examples. – Keep practicing and exploring! | As we conclude today’s lesson on solving percent equations, it’s important to recap the key points and methods we’ve covered. For homework, students are assigned a practice worksheet that will help solidify their understanding of the concepts. Encourage students to look for real-life applications of percent equations, such as calculating discounts during shopping, figuring out tax rates, or understanding interest rates on savings. This will help them see the relevance of what they’ve learned. Remind them that practice is essential for mastery, and exploring these concepts in the world around them will make the math more meaningful.