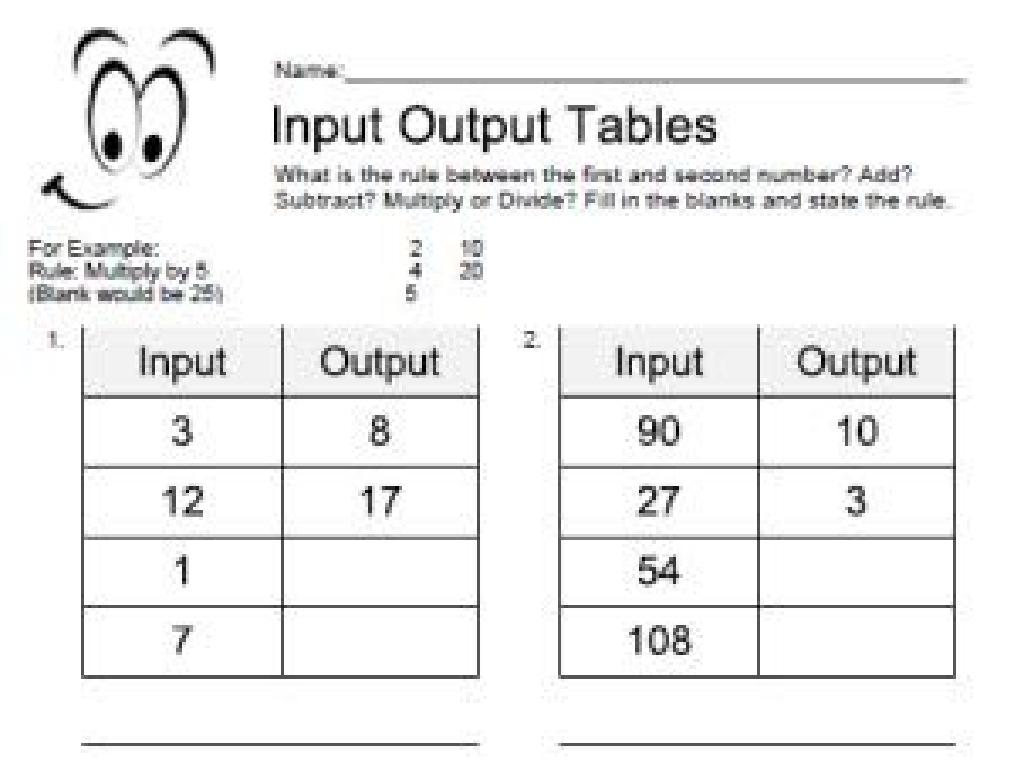
Experimental Probability
Subject: Math
Grade: Seventh grade
Topic: Probability
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Exploring Experimental Probability
– Understanding chance in probability
– Probability measures the likelihood of an event occurring.
– Defining experimental probability
– It’s determined by conducting experiments and recording outcomes.
– Real-life probability scenarios
– Coin tosses, dice rolls, and drawing cards are common examples.
– Calculating experimental probability
– Use the formula: Probability = (Number of favorable outcomes) / (Total number of trials)
|
This slide introduces students to the concept of experimental probability, which is a fundamental aspect of understanding chance and probability in mathematics. Begin by explaining that probability is a way to measure how likely it is for a certain event to happen. Experimental probability is specifically determined by performing experiments and observing the frequency of outcomes. Provide real-life examples such as the probability of getting heads in a coin toss, or the likelihood of drawing a red card from a deck. Encourage students to think of other examples from their daily lives. Conclude by showing them how to calculate experimental probability using the formula, emphasizing the importance of a large number of trials to get more accurate results. The next class will involve hands-on activities to solidify these concepts.
Understanding Probability
– Define Probability
– Probability is the measure of how likely an event is to occur.
– Theoretical vs. Experimental
– Theoretical probability is based on known values, while experimental is based on actual experiments.
– Probability measures likelihood
– It’s expressed as a number between 0 and 1, where 0 means impossible and 1 means certain.
– Real-world probability applications
– For example, flipping a coin or rolling a die.
|
Introduce the concept of probability as a fundamental aspect of mathematics that measures the likelihood of an event occurring. Explain the difference between theoretical probability, which is calculated based on known outcomes, and experimental probability, which is determined through the actual performance of an experiment. Emphasize that probability is always a number between 0 and 1, with 0 indicating an impossible event and 1 indicating a certainty. Use everyday examples such as coin tosses or dice rolls to illustrate these concepts. Encourage students to think of other real-world scenarios where probability is applicable.
Understanding Experimental Probability
– Define experiments and outcomes
– An experiment is a process with uncertain results, and outcomes are the possible results.
– Experimental Probability formula
– To calculate, divide the frequency of the event by the number of trials.
– Clarify trials, outcomes, and events
– Trials are repetitions, outcomes are results, and events are specific outcomes we’re interested in.
– Applying the formula in examples
– Let’s use the formula with real data from coin flips or dice rolls.
|
This slide introduces the concept of experimental probability, which is fundamental in understanding how often an event is likely to occur based on actual experiments rather than theoretical predictions. Start by explaining that an experiment is any procedure that can be infinitely repeated and has well-defined possible outcomes. Then, introduce the formula for experimental probability and explain each component: the number of times the event occurs (successes) and the total number of trials (repetitions of the experiment). Emphasize the difference between trials, outcomes, and events with clear examples. Finally, apply the formula to a simple experiment, such as flipping a coin or rolling a die, to solidify the students’ understanding. Encourage students to think of other examples of experiments where they can apply this concept.
Conducting Simple Probability Experiments
– Perform a coin toss experiment
– Flip a coin 50 times and tally heads or tails
– Conduct a dice roll experiment
– Roll a die 50 times and tally the numbers
– Record all possible outcomes
– List each result from the experiments
– Calculate the experimental probability
– Use the formula: Probability = (Number of favorable outcomes) / (Total number of trials)
|
This slide introduces students to the concept of experimental probability through hands-on activities. Students will perform two classic probability experiments: tossing a coin and rolling a die. They should conduct a sufficient number of trials (e.g., 50) to gather a representative sample of outcomes. After completing the experiments, students will record the outcomes and use the data to calculate the probability of each event occurring. Emphasize the importance of recording accurate data and discuss how the experimental probability may approach the theoretical probability with a larger number of trials. Encourage students to reflect on the difference between experimental and theoretical probability.
Exploring Experimental Probability
– Marble color probability
– What’s the chance of drawing a red marble from a bag with various colored marbles?
– Spinner outcome probability
– If we spin a spinner, what are the odds it lands on blue?
– More trials, more accuracy
– Performing an experiment multiple times leads to a probability closer to the true value.
– Variability of results
– Results can differ each time; this is normal in experiments.
|
This slide introduces students to the concept of experimental probability through tangible examples. Start with a simple experiment of drawing marbles from a bag, discussing the likelihood of drawing a specific color based on the total number of marbles. Move on to a spinner example, where students can predict the outcome of spinning a spinner divided into colored sections. Emphasize the importance of conducting more trials to reach a probability that is closer to the theoretical probability. Finally, discuss how results can vary with each set of trials due to the randomness inherent in experimental probability. Encourage students to think critically about how the number of trials can affect the reliability of their probability estimates.
Theoretical vs. Experimental Probability
– Expected vs. Actual Outcomes
– Theoretical: what should happen. Experimental: what actually happens.
– Reasons for differences
– Variability, measurement errors, sample size.
– Significance of many trials
– More trials, closer to theoretical probability.
– Understanding probability
|
This slide aims to explain the difference between theoretical and experimental probability. Theoretical probability is based on what is expected to happen in an ideal situation, while experimental probability is based on actual results from an experiment. Differences between these can arise due to various factors such as sample size, chance, and experimental error. Emphasize the importance of conducting a large number of trials to minimize these differences and to approach the theoretical probability more closely. This understanding is crucial for students as it lays the foundation for more complex probability concepts and helps them understand the nature of randomness and prediction in practical scenarios.
Class Activity: Probability in Action
– Conduct your own probability experiment
– Record all experimental results
– Calculate the experimental probability
Use the formula: Experimental Probability = (Number of times event occurs) / (Total number of trials)
– Share and discuss findings with the class
|
In this group activity, students will actively engage with the concept of experimental probability by conducting their own experiments in small groups. Provide students with materials like coins, dice, or cards to perform repeated trials and observe outcomes. They should record the results of each trial, then use those results to calculate the experimental probability of an event occurring. After calculations, students will present their findings to the class, fostering a discussion about the nature of probability and how it applies to real-world scenarios. As a teacher, prepare to guide them through the calculation process and facilitate the discussion, ensuring they understand the difference between theoretical and experimental probability. Possible activities include flipping coins, rolling dice, or drawing colored balls from a bag.
Wrapping Up: Experimental Probability
– Recap of experimental probability
– It’s the likelihood of an event based on trials or experiments.
– Significance in statistics
– Helps predict outcomes in real-world scenarios.
– Engage in Q&A session
– Reflect on what we’ve learned
– Think about how this applies to daily decisions.
|
As we conclude today’s lesson, we’ll revisit the concept of experimental probability, which is the chance of something happening based on repeated testing and observing results. It’s a cornerstone of statistics, providing a practical approach to predicting future events based on historical data. Encourage students to ask questions to clarify their understanding. Use this opportunity to assess comprehension and correct any misconceptions. Finally, prompt students to consider how probability plays a role in everyday decisions and future careers in fields like science, technology, and economics.