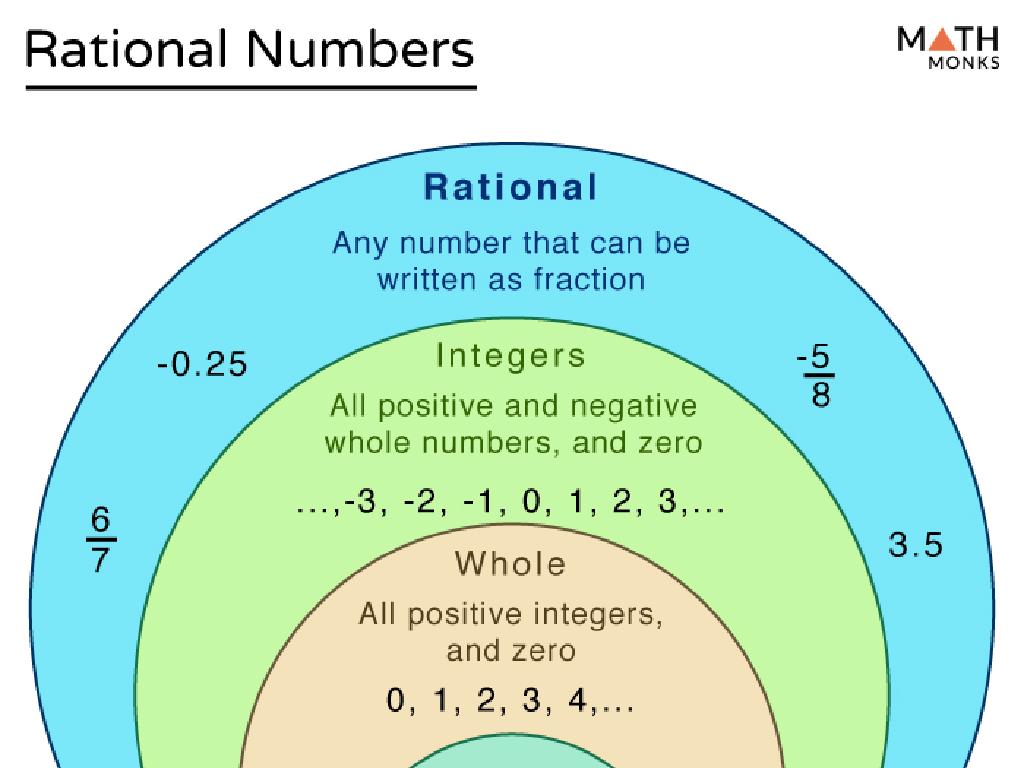
Put Rational Numbers In Order
Subject: Math
Grade: Eighth grade
Topic: Rational Numbers
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Welcome to Rational Numbers
– Define rational numbers
– Numbers expressed as a fraction of two integers
– Characteristics of rational numbers
– They have a decimal representation that is terminating or repeating
– Examples of rational numbers
– 1/2, -3/4, 0.75, -2, 5/3
– Placing rational numbers in order
– Arrange by converting to decimals or finding common denominators
|
This slide introduces the concept of rational numbers, which are any numbers that can be expressed as the quotient or fraction of two integers. The numerator and the denominator in the fraction are both whole numbers, with the denominator not being zero. Rational numbers include integers, fractions, and finite or repeating decimals. When placing rational numbers in order, students can convert them to decimals or find a common denominator to compare them directly. It’s important to provide examples that illustrate different forms of rational numbers and to practice arranging them to build a solid understanding of the concept.
Properties of Rational Numbers
– Closure Property
– Adding or multiplying two rationals always results in a rational number.
– Commutative Property
– Order doesn’t affect the sum or product of rational numbers.
– Associative Property
– Grouping doesn’t change the sum or product of rationals.
– Examples for each property
– e.g., (1/2 + 1/3) + 1/4 = 1/2 + (1/3 + 1/4); both give 13/12.
|
This slide introduces the fundamental properties of rational numbers, which are crucial for understanding how these numbers behave under different operations. The closure property ensures that the sum or product of any two rational numbers is also a rational number. For example, 1/2 + 1/3 = 5/6, which is rational. The commutative property indicates that the order in which we add or multiply rational numbers does not affect the result, such as 1/2 * 1/3 = 1/3 * 1/2. The associative property shows that the way in which numbers are grouped in addition or multiplication does not change the outcome, as demonstrated by the provided example. Encourage students to come up with their own examples to solidify their understanding.
Comparing Rational Numbers
– Compare two rational numbers
– Determine which is greater or less by converting to common denominators or decimals
– Use number lines for order
– Visualize and plot numbers to see their relative positions
– Examples of ordering numbers
– Arrange a set of rational numbers from least to greatest
– Practice with real-world problems
|
This slide introduces the concept of comparing and ordering rational numbers, which are numbers that can be expressed as a fraction or decimal. Start by explaining how to compare two rational numbers by finding a common denominator or converting them to decimals. Emphasize the use of number lines as a tool to help visualize and understand the order of numbers. Provide examples where students arrange rational numbers in ascending or descending order. Incorporate real-world problems to apply these concepts, such as comparing money amounts, distances, or measurements. Encourage students to practice these skills with additional problems to gain confidence.
Ordering Rational Numbers
– Steps to order rational numbers
– List numbers, find LCM, rewrite with common denominators
– Convert to common denominators
– Use LCM to rewrite fractions for comparison
– Arrange numbers least to greatest
– Line up numbers, compare denominators, order them
– Practice with examples
|
When teaching students to put rational numbers in order, start by explaining the steps involved in the process. Emphasize the importance of finding the least common multiple (LCM) to convert all numbers to have the same denominator, which simplifies comparison. Once converted, guide students to arrange the numbers from the smallest to the largest by comparing the numerators. Provide several examples for students to practice, starting with simple fractions and then including mixed numbers and decimals. Encourage students to work in pairs or groups to discuss their strategies and solutions, fostering collaborative learning.
Practice: Ordering Rational Numbers
– Order positive & negative fractions
– Example: Arrange -3/4, 1/2, -1/8 from least to greatest
– Mix fractions, decimals, percents
– Example: Place 3/5, 0.75, 45% in order
– Step-by-step walkthrough
– Demonstrate steps to compare and order each set
– Apply ordering in exercises
|
This slide is aimed at providing students with practical examples to reinforce their understanding of ordering rational numbers. Start with simple positive and negative fractions to ensure they grasp the concept of comparing magnitudes. Then, introduce a mixed set including fractions, decimals, and percents, which requires conversion for direct comparison. Walk the students through each example, explaining the thought process and the mathematical steps involved. Encourage students to practice these skills with additional examples and to ask questions if they encounter difficulties. This will help solidify their understanding and prepare them for more complex problems.
Class Activity: Human Number Line
– Each student is a rational number
– Form a line based on value
– Order from least to greatest
– Collaborate to find correct positions
– Discuss with peers to decide where you belong in the line
|
This interactive class activity involves students embodying rational numbers to create a human number line. Assign each student a different rational number, ensuring a mix of positive and negative fractions, decimals, and whole numbers. Students will then physically arrange themselves in order from the smallest (least) to the largest (greatest) number. This activity helps students understand the relative value of rational numbers and the concept of ordering. As a teacher, facilitate the activity by guiding students who struggle to find their correct position and ensure everyone participates. Possible variations include using number cards, having students hold signs, or creating multiple lines for different sets of numbers.
Wrapping Up: Rational Numbers
– Recap of ordering rational numbers
– Understanding rational numbers is key
– Grasping these concepts is crucial for future math topics.
– Homework: Ordering worksheet
– Complete the provided worksheet to practice.
– Practice makes perfect!
|
As we conclude today’s lesson on rational numbers, it’s important to review the key concepts and methods we’ve used to put rational numbers in order. Understanding how to compare and sequence rational numbers is essential as it forms the foundation for more advanced mathematical concepts. For homework, students are assigned a worksheet that will reinforce today’s lesson by providing additional practice in ordering rational numbers. Encourage students to attempt all problems and remind them that consistent practice is vital for mastering this skill. In the next class, we will review the homework answers and address any questions or difficulties encountered.