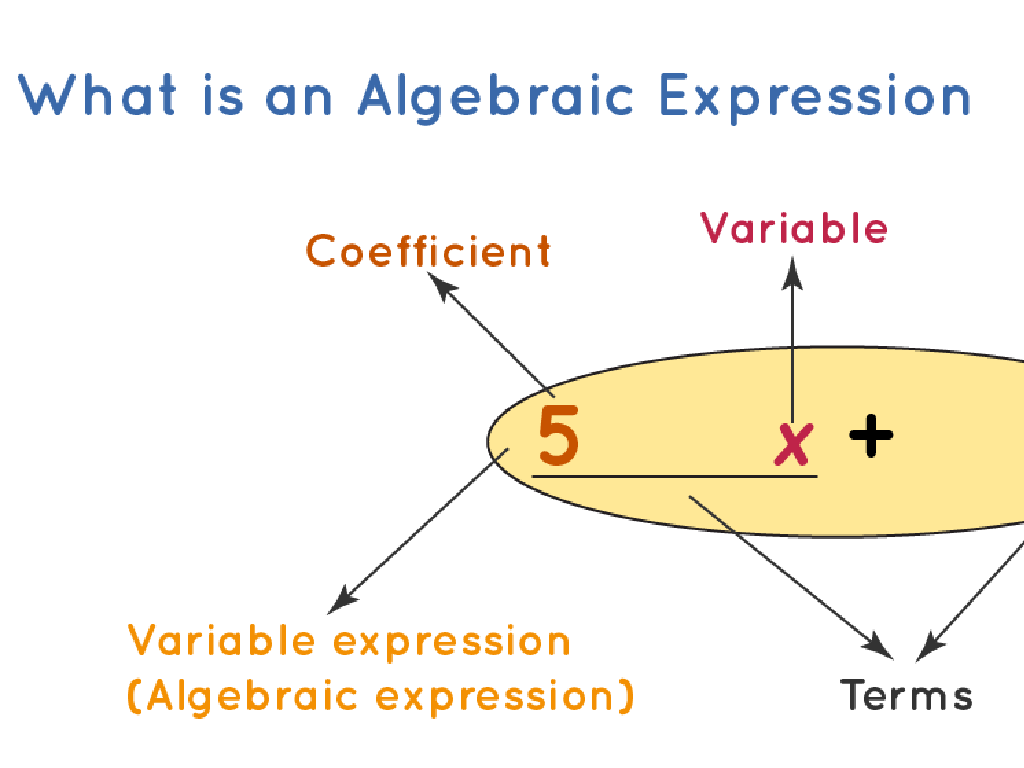
Compare And Order Rational Numbers Using Number Lines
Subject: Math
Grade: Sixth grade
Topic: Rational Numbers
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Welcome to Rational Numbers!
– What are Rational Numbers?
– Numbers that can be expressed as a fraction a/b, where a and b are integers and b is not zero.
– Characteristics of Rational Numbers
– They include integers, fractions, and terminating or repeating decimals.
– Identifying Rational Numbers
– Examples: 1/2, 3, 0.75, -6, 4.333…
– Rational Numbers on a Number Line
– Visualize and compare by placing them on a number line.
|
This slide introduces the concept of rational numbers, which are any numbers that can be written as a fraction with integers in the numerator and denominator, the latter being non-zero. It’s important for students to recognize that this includes whole numbers, fractions, and decimals that either terminate or repeat. Provide examples of each type and show how they can be represented on a number line. This visual representation will help students understand how to compare and order rational numbers, which is a foundational skill in mathematics. Encourage students to think of their own examples of rational numbers and to practice placing them on a number line.
Understanding Rational Numbers
– Rational number definition
– A number expressible as a fraction a/b, where a and b are integers and b ` 0
– Examples of rational numbers
– 1/2, 3/4, 5 (which is 5/1), and 0.75 (which is 3/4)
– Non-examples to clarify
– Numbers like Pi (À) and 2 are not rational
– Visualizing on number lines
|
Introduce the concept of rational numbers by defining them as numbers that can be written as fractions with integer numerators and non-zero integer denominators. Provide clear examples of rational numbers, including both fractions and decimals that can be converted to fractions. Contrast these with non-examples such as Pi and the square root of 2, which cannot be expressed as fractions with integer terms, to solidify understanding. Emphasize that rational numbers can be represented on a number line, which will be explored in subsequent slides. Encourage students to think of other examples and non-examples to discuss.
Understanding Rational Numbers on a Number Line
– Define a number line
– A straight line with numbers placed at equal intervals
– Representing rational numbers
– Rational numbers are shown as points on the line
– Placing positive rational numbers
– Positive numbers are to the right of zero
– Placing negative rational numbers
– Negative numbers are to the left of zero
|
This slide introduces students to the concept of a number line and how it is used to represent rational numbers, which include both positive and negative numbers as well as fractions and decimals. Begin by defining a number line as a visual representation of numbers in a sequential order. Demonstrate how to place rational numbers on the number line by marking points that correspond to their value. Emphasize the position of positive numbers to the right of zero and negative numbers to the left. Use examples like 1/2, 3/4, -1/2, and -3/4 to show exact placement on the number line. Encourage students to practice by giving them a range of rational numbers to place on a number line themselves.
Comparing Rational Numbers on a Number Line
– Use number lines for comparison
– Visualize and determine which numbers are larger or smaller
– Understand >, <, and = symbols
– Symbols represent relationships between numbers
– Compare 1/2 and 3/4
– 1/2 is less than 3/4 on a number line
– Compare -1/3 and -1/2
– -1/3 is greater than -1/2 on a number line
|
This slide introduces students to the concept of comparing rational numbers using number lines. Emphasize the importance of visual representation for understanding the size of different numbers. Explain the meaning of greater than (>) and less than (<) symbols, as well as the equal to (=) sign. Use the examples provided to show how to place and compare fractions on a number line, highlighting that 3/4 is closer to 1 than 1/2, and -1/3 is closer to 0 than -1/2, making it larger in the context of negative numbers. Encourage students to practice with additional examples and to draw their own number lines for better comprehension.
Ordering Rational Numbers on a Number Line
– Arrange numbers from least to greatest
– Place rational numbers in order on a number line
– Absolute value in ordering
– Absolute value determines distance from zero
– Activity: Order given rational numbers
– Use a number line to order -3/4, 1/2, -1 1/3, and 2/5
|
This slide introduces students to the concept of ordering rational numbers. Start by explaining how to arrange numbers from the smallest to the largest, using a number line as a visual aid. Discuss the role of absolute value in determining a number’s position relative to zero, regardless of its sign. For the activity, provide students with a set of rational numbers and ask them to arrange them on a number line. This hands-on activity will help solidify their understanding of the concept. Encourage students to think about the size of fractions and the role of negative signs while ordering. The teacher should prepare to guide students through the activity, offering examples of how to determine the correct order and how to use absolute value in the process.
Class Activity: Number Line Challenge
– Receive a set of rational number cards
– Create a number line on your desk
– Order numbers on your number line
– Class review and discussion
– Discuss any difficulties or different methods used
|
This interactive activity is designed to help students understand the concept of ordering rational numbers on a number line. Each student will be given a set of cards with different rational numbers. They will then use these cards to create a number line on their desks, placing the numbers in the correct order. After everyone has completed their number line, the class will come together to review the results. During the discussion, encourage students to talk about the challenges they faced and the strategies they used to determine the correct order. This will help them to learn from each other and to understand different approaches to the task. Possible variations of the activity could include using negative numbers, fractions, or decimals to increase the complexity for advanced students.
Wrapping Up: Rational Numbers
– Recap: Comparing & Ordering
– Review how to use number lines for rational numbers
– Why master this skill?
– Essential for advanced math concepts
– Homework: Practice Worksheet
– Complete the worksheet on rational numbers
– Next class: Q&A Session
– Bring questions for review
|
As we conclude today’s lesson, remind students of the key concepts in comparing and ordering rational numbers using number lines. Emphasize the importance of mastering this skill as it is foundational for understanding more complex mathematical concepts in the future. For homework, assign a worksheet that provides additional practice on this topic to reinforce learning. In the next class, we will have a Q&A session to address any uncertainties or difficulties students may have encountered while completing the worksheet. This will ensure that all students are confident in comparing and ordering rational numbers before moving on to the next topic.