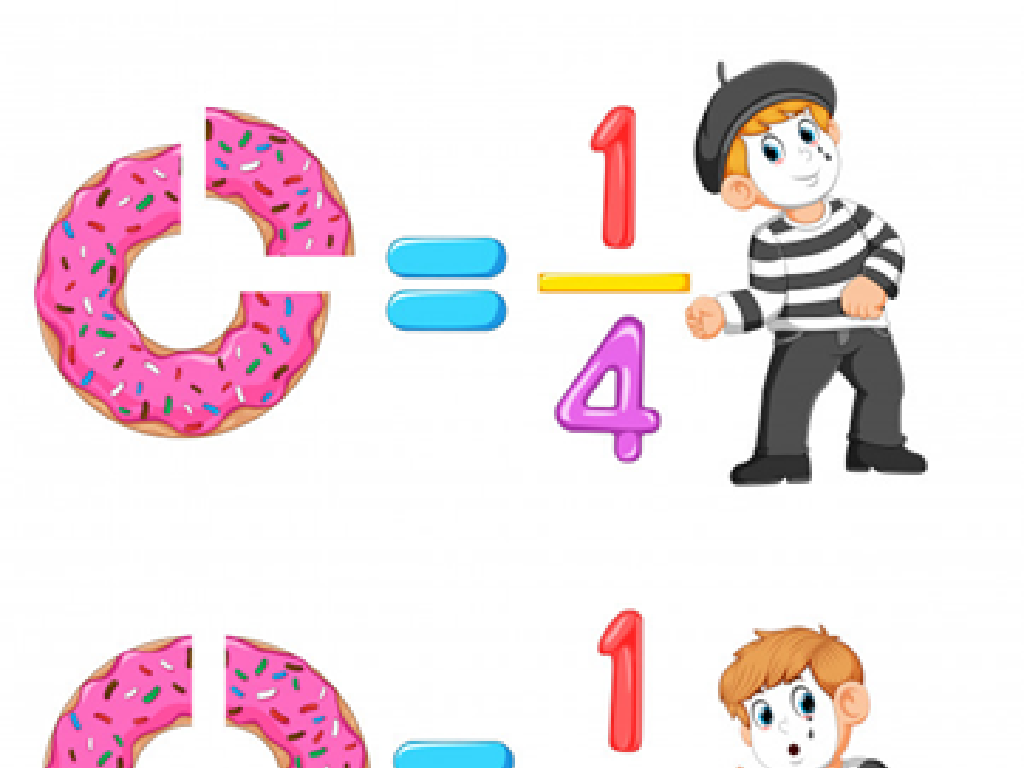Your next great Lessn starts here.

Welcome to Scaling Fractions! – Quick recap of fractions – Fractions represent parts of a whole – Understanding the concept of scaling – Scaling means resizing something proportionally – Learning to scale fractions by fractions – Multiply fractions to find a scaled version – Setting goals for today’s lesson | Begin the lesson with a brief review of fractions to ensure students recall that fractions represent parts of a whole. Introduce the concept of scaling as a way to proportionally increase or decrease the size of an object or number. Today’s objective is to learn how to apply the concept of scaling to fractions by multiplying a fraction by another fraction. This skill is essential for understanding proportional relationships and for solving real-world problems involving fractions. Encourage students to think of scaling as resizing something, like blowing up a balloon or shrinking an image, but with numbers. Make sure to provide examples and practice problems to solidify their understanding.

Recap: Understanding Fractions – A fraction is part of a whole – Like a slice of pizza from a whole pie – Numerator and denominator explained – Top number (numerator) shows how many parts we have. Bottom number (denominator) shows how many equal parts the whole is divided into. – Examples: 1/2, 3/4, 5/8 – Common fractions we see in daily life | Begin the lesson by recapping the concept of fractions, ensuring that students remember that a fraction represents a portion of a whole item or set. Clarify the roles of the numerator and the denominator, using visual aids like pie charts or pizza slices to illustrate the concept. Provide familiar examples of fractions to help solidify their understanding. This foundational knowledge is crucial as it sets the stage for learning about scaling fractions by fractions, which will build on their understanding of basic fractions.

Understanding Scaling with Fractions – Scaling means resizing – Multiply numbers by fractions – In math, scaling is like ‘stretching’ or ‘shrinking’ a number – Example: 2 scaled by 1/2 – 2 * 1/2 = 1 shows how 2 is halved – Scaling changes the size | This slide introduces the concept of scaling in mathematics, specifically scaling by fractions. Scaling is a fundamental concept that involves resizing an object or quantity. When we scale a number by a fraction in math, we are essentially multiplying the original number by that fraction, which can result in the number becoming larger or smaller akin to stretching or shrinking. For example, when we scale the number 2 by the fraction 1/2, we are finding what half of 2 is, which is 1. It’s important for students to understand that scaling by a fraction less than 1 will reduce the size of the number, while scaling by a fraction greater than 1 will increase it. Encourage students to think of scaling as a transformation that changes the size of a quantity in a proportional manner.

Scaling Fractions by Whole Numbers – Review fraction multiplication – Multiply fractions by whole numbers – Example: Scale 1/3 by 3 – 1/3 times 3 equals 1 (1/3 * 3 = 1) – Understand scaling results – Scaling can result in a whole number | Begin with a quick review of how to multiply fractions by whole numbers, ensuring that students recall the process. Then, move on to the concept of scaling, which in this context means multiplying a fraction by a whole number to ‘scale it up’ or increase its size. Use the example of scaling 1/3 by 3 to show that the result can be a whole number. Emphasize that scaling is a form of multiplication that changes the size of the fraction. Encourage students to think of real-life situations where they might need to scale fractions, such as adjusting a recipe. Provide additional examples for practice, such as scaling 1/4 by 4 or 1/2 by 2, and ask students to predict the outcomes before solving.

Scaling Fractions by Fractions – Multiply two fractions together – To scale, we perform fraction multiplication – Combine numerators and denominators – Multiply tops (numerators), multiply bottoms (denominators) – Example: Scaling 1/2 by 3/4 – 1/2 * 3/4 = (1*3)/(2*4) = 3/8 | When we talk about scaling fractions by fractions, we’re essentially discussing how to multiply two fractions. This is a fundamental skill in math that allows students to understand how quantities change when they are scaled. To multiply fractions, students should multiply the numerators (the top numbers) to get the new numerator, and multiply the denominators (the bottom numbers) to get the new denominator. For example, when scaling 1/2 by 3/4, we multiply 1 by 3 to get 3, and 2 by 4 to get 8, resulting in the fraction 3/8. It’s important to walk through this process step by step, ensuring that students grasp the concept of scaling as multiplication. Encourage students to practice with different fractions to become comfortable with the process.

Let’s Practice: Scaling Fractions by Fractions – Scale 2/3 by 1/2 example – Multiply 2/3 by 1/2 to scale the fraction – Scale 5/8 by 3/5 example – Multiply 5/8 by 3/5 to find the scaled fraction – Class activity: work through examples – We’ll solve these examples together in class – Understand scaling concept | This slide is designed to provide students with hands-on practice in scaling fractions by fractions. Start by explaining that scaling a fraction by another fraction means multiplying the two fractions. Work through the first example by multiplying 2/3 by 1/2, which equals 1/3 after simplification. Then, move on to the second example, multiplying 5/8 by 3/5 to get 15/40, which simplifies to 3/8. Encourage students to participate in solving these problems as a class activity. This will help them understand the concept of scaling and how it applies to fractions. Make sure to provide guidance and support as they work through the examples, and clarify any misconceptions. The goal is for students to become comfortable with the process of scaling fractions by fractions.

Scaling Fractions in Real Life – Scaling in cooking recipes – Halving or doubling a recipe adjusts ingredient amounts. – Scaling in construction work – Blueprints show a smaller version of buildings. – Scaling in art and design – Artists resize images to create balance. – Understanding scaling importance | This slide aims to show students how scaling fractions are applied in everyday life. In cooking, recipes are often scaled up or down to accommodate the number of servings needed, which involves multiplying or dividing the quantities of ingredients, which are often fractions. In construction, blueprints are a scaled-down representation of the actual structure, requiring workers to scale up measurements to build correctly. In art, scaling is important for resizing images while maintaining proportionality. Understanding these applications helps students see the relevance of math in the real world and grasp the concept of scaling fractions by fractions.

Class Activity: Fraction Scaling Challenge – Scale given fractions by other fractions – Use fraction strips or grids for help – Visual aids make understanding fractions easier – Present your findings to the class – Collaborate and learn with your group – Discuss strategies and solutions with peers | This activity is designed to help students understand the concept of scaling fractions by using other fractions. Divide the class into small groups and provide each group with a set of fractions to scale. Encourage the use of fraction strips or grids to visually represent the fractions and the scaling process. After completing the activity, each group will present their results to the class, explaining the method they used. This will foster a collaborative learning environment where students can learn from each other. Possible activities include scaling recipes, comparing distances, or adjusting measurements in a craft project. The goal is for students to apply the concept of fraction scaling to real-world scenarios and to become comfortable with multiplying fractions.

Wrapping Up: Scaling Fractions – Recap: Scaling with fractions Remember how to multiply fractions to scale them. – Homework: Practice worksheet Complete the worksheet to master scaling. – Quiz preparation Study for a quiz on scaling fractions. – Key takeaways review | As we conclude today’s lesson on scaling fractions by fractions, remind students of the main points: multiplying fractions to increase or decrease their size, and how this concept applies to real-world problems. Assign a practice worksheet for homework to reinforce these skills. Let students know that there will be a quiz in the next class to assess their understanding of scaling fractions. Encourage them to review their notes, the practice worksheet, and to ask questions if they need clarification on any concepts.