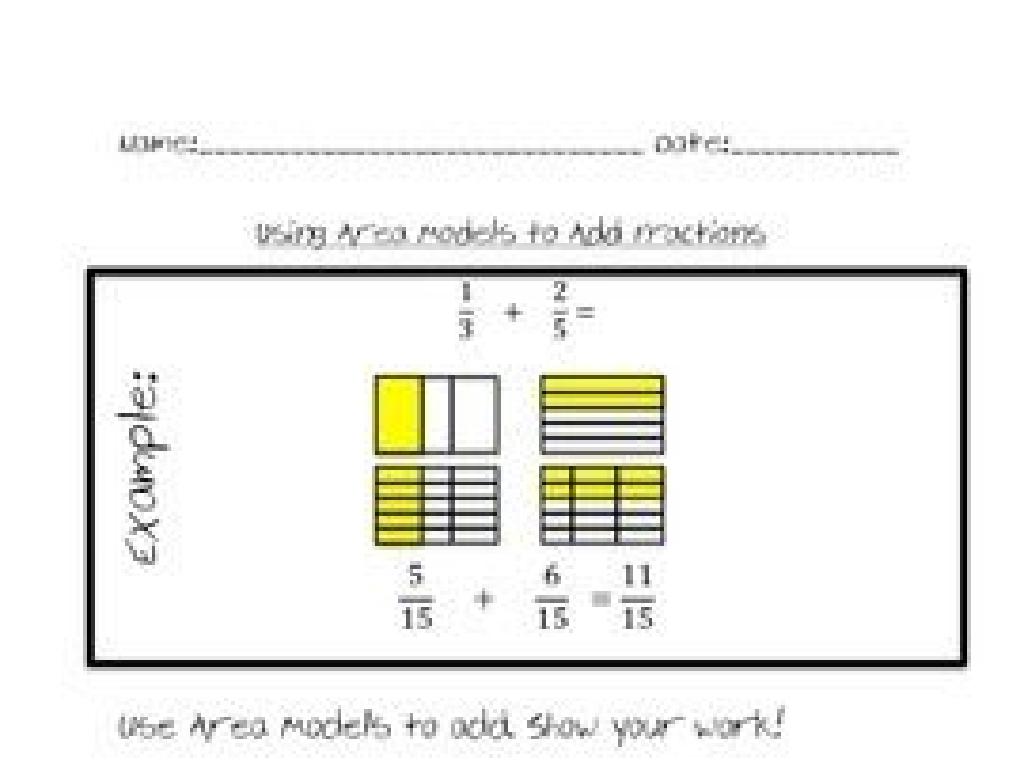
Find The Slope From A Table
Subject: Math
Grade: Eighth grade
Topic: Slope
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Welcome to Slope: Understanding its Role
– Grasping slope in daily life
– Slope is seen in ramps, roofs, and even slides.
– Defining slope
– Slope is the steepness of a line, a ratio of rise over run.
– Why slope matters in math
– It’s crucial for graphing lines and predicting trends.
– Exploring slope with tables
– Learn to calculate slope from pairs of points in a table.
|
This slide introduces the concept of slope and its significance in both everyday life and mathematics. Begin by discussing how slope is observed in various real-world structures and how it affects their design and function. Then, define slope mathematically as the measure of the steepness of a line, expressed as a ratio. Emphasize the importance of slope in graphing linear equations, understanding geometric relationships, and analyzing data. Conclude by explaining how students can find the slope by examining changes in y-values over changes in x-values within a table of values. Encourage students to think of examples of slope they encounter daily and prepare them for hands-on activities involving slope calculations from tables.
Understanding Slope from Tables
– Review tables and graphs
– Tables display numerical information organized in rows and columns.
– Reading data from tables
– Identify the x (input) and y (output) values in the table.
– Math table examples
– Temperature over a week, points scored in games.
– Finding slope in tables
– Calculate the change in y over the change in x.
|
This slide aims to reinforce the students’ understanding of tables and how to interpret them, which is essential for finding the slope from a table. Begin by reviewing the structure of tables and graphs, emphasizing their role in organizing data. Show students how to read and extract data points from tables, focusing on the x and y values. Provide clear examples of tables used in math, such as tracking temperature changes over time or points scored in a series of games. Finally, guide students through the process of finding the slope by calculating the rate of change in the y-values relative to the x-values. Encourage students to practice with different tables to become comfortable with the concept of slope.
Slope Basics: Understanding Slope in Math
– Define slope in math
– Slope measures steepness of a line: rise over run
– Slope formula explained
– Use (y2 – y1) / (x2 – x1) to calculate slope between two points
– Positive vs Negative slope
– Positive slope rises, negative slope falls
– Slope interpretation in graphs
– Slope indicates direction and steepness of a line on a graph
|
This slide introduces the concept of slope, which is a fundamental aspect of algebra and geometry. Slope is the measure of the steepness or incline of a line, often described as ‘rise over run.’ The formula (y2 – y1) / (x2 – x1) is used to calculate the slope between two points on a coordinate plane. Positive slopes indicate a line rising from left to right, while negative slopes indicate a line falling from left to right. Understanding the concept of slope is crucial for students as it applies to various aspects of mathematics, including graphing linear equations and interpreting data. Encourage students to practice calculating slope from tables of values and to recognize the significance of the slope in real-world contexts, such as in construction and road design.
Finding Slope from a Table
– Identify coordinates in a table
– Locate and write down pairs of x and y from the table
– Apply the slope formula
– Use (y2 – y1) / (x2 – x1) to calculate slope
– Work through a practice example
– Use a given table to find the slope step by step
– Understand slope in real-world contexts
– Relate slope to scenarios like hiking trails’ steepness
|
This slide introduces the concept of finding the slope from a table, a key skill in understanding linear relationships in algebra. Start by explaining how to identify coordinate pairs (x, y) in a table. Then, demonstrate the slope formula, (y2 – y1) / (x2 – x1), and how to apply it using the coordinates. Provide a practice example with table data for students to work through, reinforcing the lesson. Finally, connect the concept to real-world situations, such as determining the steepness of a hill, to help students see the practical application of slope. Encourage students to ask questions and work through the practice example in pairs or small groups for collaborative learning.
Finding the Slope from Tables
– Work through Example 1 with Table A
– Calculate the rise over run between points in Table A
– Work through Example 2 with Table B
– Calculate the rise over run between points in Table B
– Discuss slope patterns
– Identify how the slope is consistent between different intervals
– Understand slope consistency
– Recognize that the slope is the same regardless of the points chosen
|
This slide aims to provide students with clear examples of how to calculate the slope from a set of data in a table. Start with Example 1 by demonstrating how to find the difference in the y-values (rise) and the difference in the x-values (run) between two points in Table A. Repeat the process with Example 2 using Table B. Emphasize the pattern that emerges when calculating slope and how it remains consistent across different pairs of points. This will help students understand that the slope of a linear relationship is constant, which is a fundamental concept in algebra. Encourage students to practice with additional tables to reinforce the concept.
Class Activity – Find the Slope!
– Work in pairs for group activity
– Each pair gets a unique values table
– Calculate the slope from the table
– Use the formula (y2 – y1) / (x2 – x1)
– Present your findings to the class
|
This interactive class activity is designed to help students apply their knowledge of slopes to real data. Organize the class into pairs, providing each pair with a unique table of values. Instruct them to calculate the slope by using the formula (change in y) / (change in x), or (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) are two points from the table. After calculations, each pair will present their findings, explaining how they determined the slope. This will foster collaborative learning and enhance their understanding of slopes in a practical context. Possible variations of the activity could include tables with positive, negative, zero, or undefined slopes to cover different scenarios.
Conclusion: Understanding Slope from Tables
– Recap: Finding slope from a table
– Review steps: Calculate rise over run between points
– Slope’s role in various fields
– Used in physics, economics, and geography
– Q&A session
– Clarify doubts and reinforce learning
– Review key takeaways
|
As we conclude, revisit the method to find the slope from a table by calculating the vertical change (rise) over the horizontal change (run) between two points. Emphasize the importance of slope in real-world applications such as physics for motion, economics for cost analysis, and geography for terrain assessment. Encourage students to ask questions to clear up any confusion. Use this time to solidify their understanding and ensure they grasp the concept of slope as it relates to interpreting and creating graphs from data tables.