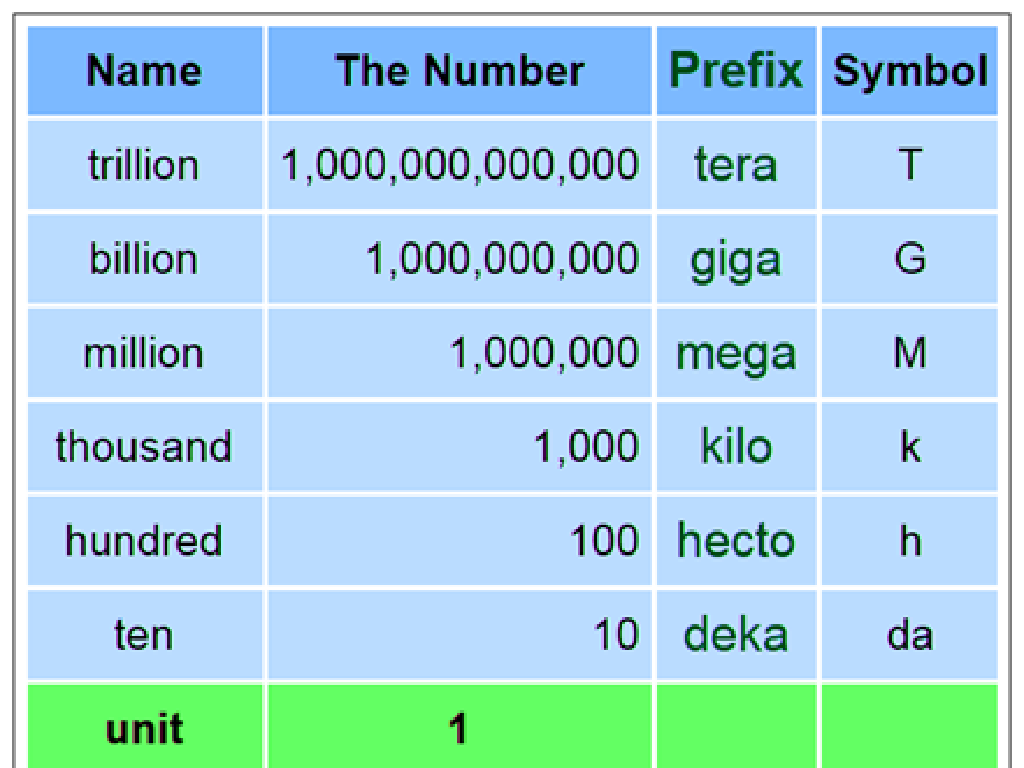
Estimate Cube Roots
Subject: Math
Grade: Eighth grade
Topic: Square Roots And Cube Roots
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Introduction to Cube Roots
– Understanding cube roots
– Cube roots are the inverse of cubing a number
– Defining a cube root
– A cube root of a number is a value that, when cubed, gives the original number
– Cube roots in real life
– Volume of cubes, earthquakes’ intensity on Richter scale
– Estimating cube roots
– Use estimation to find a cube root close to a whole number
|
Begin with a brief review of square roots to build a foundation for understanding cube roots. Explain that cube roots are similar but instead of finding a number that multiplies by itself twice (square root), we are looking for a number that multiplies by itself three times (cube root). Provide relatable examples such as calculating the volume of a cube when given the volume or understanding the magnitude of an earthquake. Teach students how to estimate cube roots by finding two perfect cubes between which the number lies, and then hone in on the more precise value. This concept will be crucial for solving real-world problems and understanding the geometry of three-dimensional shapes.
Visualizing Cube Roots
– Visualize cubes and roots
– Definition of cube root
– A number that multiplies by itself thrice to give the original number.
– Cube root of 27 is 3
– 3^3 (3*3*3) equals 27, so cube root of 27 is 3
– Practice with different numbers
– Find cube roots for 8, 64, and 125
|
This slide introduces the concept of cube roots through visual representation and definition. Start by explaining that a cube root of a number is a value that, when used in a multiplication three times, results in the original number. Use the example of 27 to show that 3 multiplied by itself three times equals 27, making 3 the cube root of 27. Encourage students to visualize this process with cubes, if possible. After explaining the concept, provide practice problems with different numbers such as 8, 64, and 125 to solidify their understanding. The goal is for students to be able to estimate cube roots by recognizing patterns and using simple multiplication.
Estimating Cube Roots
– Estimating without a calculator
– Use nearest perfect cubes
– Find perfect cubes close to the number, like 3^3=27 and 4^3=64 for 50
– Example: Cube root of 50
– Since 50 is between 27 and 64, the cube root of 50 is between 3 and 4
– Practice estimation skills
|
This slide introduces students to the concept of estimating cube roots without the use of a calculator. Emphasize the importance of knowing perfect cubes to make accurate estimations. For example, to estimate the cube root of 50, students should recognize that 50 falls between the perfect cubes of 27 (3 cubed) and 64 (4 cubed). Therefore, the cube root of 50 is between 3 and 4. Encourage students to practice this skill with different numbers to become proficient at estimating cube roots. Provide additional examples and exercises for students to work on, such as estimating the cube root of 30 or 70, to reinforce the concept.
Estimating Cube Roots
– Perfect cubes up to 10^3
– 1^3=1, 2^3=8, …, 10^3=1000
– Grasping non-perfect cubes
– Non-perfect cubes don’t have whole number roots
– Estimating roots of non-perfect cubes
– Find two perfect cubes between which the number lies
– Practice with examples
– Use estimation to find cube roots of 1728, 500
|
This slide introduces students to the concept of perfect and non-perfect cubes, providing a foundation for understanding cube roots. Start by listing the perfect cubes from 1 to 10, which will serve as reference points for estimating the cube roots of non-perfect cubes. Explain that non-perfect cubes are numbers that are not the exact cube of a whole number, and their cube roots are not whole numbers. Teach students how to estimate the cube root of a non-perfect cube by finding the two closest perfect cubes it lies between. For example, to estimate the cube root of 500, note that 7^3=343 and 8^3=512, so the cube root of 500 is between 7 and 8. Provide practice problems to reinforce the concept.
Practice Estimation of Cube Roots
– Estimating cube root of 125
– Cube root of 125 is close to 5, because 5^3 = 125
– Estimating cube root of 200
– Cube root of 200 is between 5 and 6, closer to 6 because 6^3 = 216
|
This slide is designed for a hands-on practice session on estimating cube roots. Start by reminding students that the cube root of a number is a value that, when multiplied by itself three times, gives the original number. For example 1, guide students to see that since 5 cubed (5^3) equals 125, the cube root of 125 is exactly 5. For example 2, help them understand that since 200 is between 5^3 (125) and 6^3 (216), its cube root must be between 5 and 6, and closer to 6. Encourage students to use this method to estimate cube roots of other numbers, understanding that it’s a way to find an approximate value without a calculator. Provide additional examples if time allows and encourage students to explain their reasoning.
Cube Root Estimation Game
– Pair up for cube root estimation
– Use graph paper for visualization
– Draw cubes on graph paper to help estimate the roots visually
– Estimate cube roots of assigned numbers
– Share estimates with the class
|
This interactive class activity is designed to help students understand the concept of cube roots through estimation. Students will pair up, fostering collaboration and discussion. Provide each pair with graph paper and a list of numbers for which they need to estimate the cube roots. Encourage them to draw cubes on the graph paper to visualize the concept better. After they have made their estimates, ask them to share their results with the class, explaining their estimation process. This will help reinforce their understanding and allow them to learn from each other’s strategies. As a teacher, be prepared to guide them through the estimation process and provide feedback on their techniques. Possible variations of the activity could include estimating cube roots using number lines or comparing their estimates to actual cube roots calculated with a calculator.
Estimating Cube Roots: Conclusion
– Recap cube root estimation
– Review steps to estimate cube roots of numbers
– Cube roots in real-world problems
– Practical uses like volume calculations
– Homework: Estimate 3 cube roots
– Find objects, estimate their volume’s cube root
|
As we conclude, let’s recap the process of estimating cube roots, which is a valuable skill in mathematics, especially in geometry and algebra. Understanding how to estimate cube roots can help students solve real-world problems involving volume and density. For homework, students should find three items, such as a box or a ball, estimate their volume and then find the cube root of those volumes. This exercise will reinforce their understanding and provide practical experience in estimation. Encourage students to use objects of different sizes to challenge themselves. In the next class, we’ll review their estimates and discuss any difficulties they encountered.