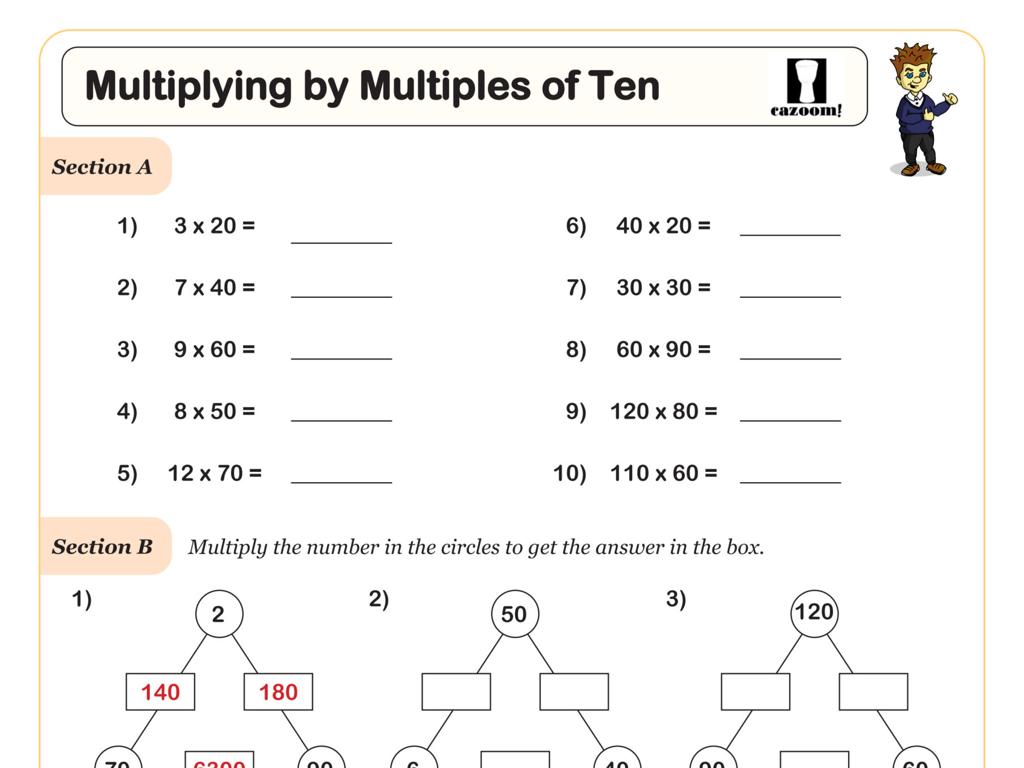
Calculate Quartiles And Interquartile Range
Subject: Math
Grade: Sixth grade
Topic: Statistics
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Quartiles and Interquartile Range in Statistics
– What are Quartiles?
– Quartiles divide data sets into four equal parts.
– Calculating Quartiles
– Find Q1, Q2 (median), and Q3 by ordering data and splitting into quarters.
– Interquartile Range (IQR)
– IQR is the difference between Q3 and Q1, showing spread of the middle half.
– Real-Life Importance
– Quartiles help us understand data distribution and identify outliers.
|
Introduce the concept of quartiles as a way to understand the distribution of a data set by dividing it into four equal parts. Explain the process of calculating quartiles: Q1 is the median of the lower half of the data, Q2 is the median of the entire set, and Q3 is the median of the upper half. Emphasize the importance of the interquartile range as a measure of variability that indicates the range within which the central 50% of the data lies. Discuss how understanding quartiles can help in real-life situations, such as determining income distribution or test scores. Provide examples and encourage students to practice calculating quartiles and IQR with different data sets.
Understanding Quartiles in Data
– Definition of Quartiles
– Quartiles are values dividing a data set into four equal parts.
– The Three Main Quartiles
– Q1 (25th percentile), Q2 (median, 50th percentile), Q3 (75th percentile).
– Quartiles Split Data into Four
– Each quartile represents 25% of the data set, showing distribution.
– Quartiles’ Role in Statistics
|
Begin with explaining that quartiles are statistical measures that divide a set of numbers into four equal parts, or quarters. Each quartile represents a quarter of the dataset. Q1 is the median of the first half of the data, Q2 is the median of the entire set, and Q3 is the median of the second half. Emphasize that quartiles are useful for understanding the spread and center of the data, and they are essential for calculating the interquartile range, which measures the middle 50% of the data. Provide examples with small data sets for clarity, and prepare to demonstrate how to calculate each quartile in the following slides.
Calculating Quartiles in Statistics
– Steps to find quartiles
– Sort data, divide into halves, find median (Q2), then Q1 and Q3
– Example: Data set quartiles
– Given set: 4, 8, 15, 16, 23, 42. Find Q1, Q2, Q3
– Practice problem together
– Use your own data set to find quartiles
– Understanding interquartile range
– IQR = Q3 – Q1, measures spread of the middle 50%
|
This slide introduces the concept of quartiles, which are values that divide a data set into quarters. Start by explaining the step-by-step method to find quartiles: organize the data in ascending order, find the median (Q2), and then determine the lower quartile (Q1) and upper quartile (Q3). Use a clear example with a simple data set to illustrate how to find Q1, Q2, and Q3. Then, engage students with a practice problem where they can apply the method to a new set of data. Finally, explain the interquartile range (IQR) as a measure of the middle 50% of the data, calculated by subtracting Q1 from Q3. The notes should guide the teacher through the process and suggest encouraging students to work in pairs or groups for the practice problem to foster collaborative learning.
Understanding Interquartile Range (IQR)
– Define Interquartile Range (IQR)
– IQR is the middle 50% of a data set, between Q1 and Q3
– IQR vs. Range: Measuring Spread
– Unlike range, IQR is resistant to outliers and gives a better sense of data spread
– How to Calculate IQR
– Subtract the first quartile (Q1) from the third quartile (Q3): IQR = Q3 – Q1
– IQR in Practice
– Use IQR to find which values fall into the middle 50% of the data
|
The slide introduces the concept of Interquartile Range (IQR) as a statistical measure used to describe the spread of the middle half of a data set. Emphasize that IQR is preferred over the range when dealing with outliers, as it provides a more accurate representation of a typical data spread. Demonstrate the calculation of IQR by finding the first (Q1) and third (Q3) quartiles and subtracting Q1 from Q3. Provide examples with actual data sets to show how IQR is used in practice. Encourage students to work on examples in groups, and prepare a few different data sets for them to analyze. This will help them understand the concept of IQR and how it can be applied to real-world situations.
Real-World Applications of Quartiles
– Quartiles in everyday life
– Used to summarize large data sets, like test scores or temperatures
– Interpreting quartiles
– Understand how quartiles divide data into groups
– Activity: Find quartiles in data
– Use the provided data sets to calculate Q1, Q2, Q3
– Discussing quartile implications
– What do the quartiles tell us about the data set?
|
Quartiles are a key concept in statistics, used to understand and interpret large sets of data by dividing them into four equal parts. This slide aims to show students the practical applications of quartiles in real life, such as analyzing test scores, weather patterns, or economic data. The activity involves students calculating the first (Q1), second (Q2), and third (Q3) quartiles of provided data sets, which will help them grasp the concept of data segmentation. Teachers should prepare several data sets for the activity, ensuring a variety of contexts to illustrate how quartiles can lead to different interpretations. Encourage students to discuss what each quartile reveals about the overall data distribution. Possible activities could include analyzing class test scores, heights of students, or daily temperatures over a month.
Class Activity: Quartile Quest!
– Divide into groups for quartile calculations
– Calculate quartiles of your data set
– Use the method learned to find Q1, Q2, Q3
– Share findings with the class
– Each group presents their quartiles
– Discuss quartile insights on data
– Reflect on data distribution and outliers
|
In this engaging class activity, students will apply their knowledge of quartiles by working in small groups. Each group will receive a different data set to analyze. They will calculate the first (Q1), second (Q2), and third (Q3) quartiles, which will help them understand the spread and central tendency of their data. After calculations, groups will share their results with the class, fostering a collaborative learning environment. The discussion will focus on how quartiles can provide insights into the data set, such as identifying outliers and understanding the distribution. Teachers should circulate to provide guidance and ensure each group understands the process. Possible activities: 1) Comparing heights, 2) Analyzing test scores, 3) Measuring time spent on homework, 4) Recording daily temperatures.
Conclusion: Quartiles & IQR in Statistics
– Recap: Quartiles & IQR definition
– Quartiles divide data into 4 equal parts; IQR measures spread between Q1 & Q3
– Significance of quartiles in data
– Quartiles help describe data distribution & identify outliers
– Addressing unanswered questions
– Review key takeaways
– Summarize how to calculate and interpret quartiles and IQR
|
As we wrap up, revisit the definitions of quartiles and the interquartile range (IQR), emphasizing their roles in summarizing data sets. Highlight the importance of quartiles in providing a deeper understanding of the distribution of data, particularly in spotting outliers and understanding the spread of the middle half of the data. Encourage students to ask any lingering questions they might have for clarification. Conclude by summarizing the main points of the lesson, ensuring students are comfortable with calculating quartiles and IQR and know how to interpret them in the context of data analysis. Prepare to provide examples or further explanation if needed during the Q&A session.