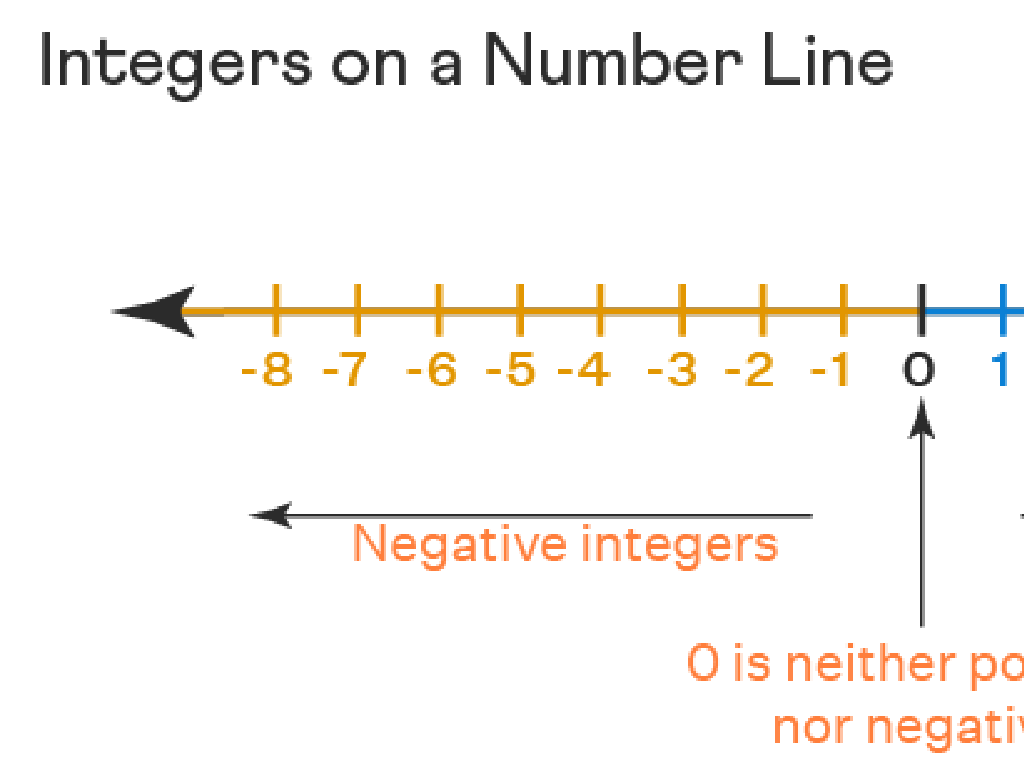Your next great Lessn starts here.

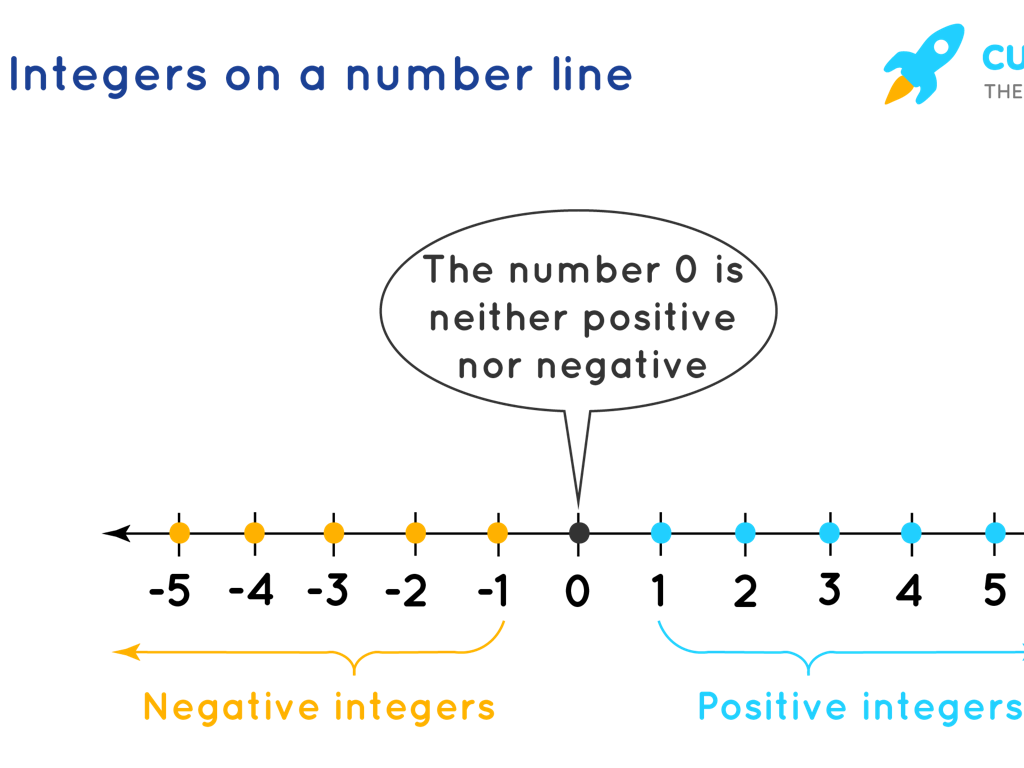
Understanding the Median in Statistics – What is the median? – The median is the middle number in an ordered list of numbers. – Statistics in daily life – Use statistics to make informed decisions, like finding the average score in games. – Steps to find the median – Sort numbers, count them, and find the middle one or average of two middle numbers. – Practice finding the median | This slide introduces the concept of the median as a part of statistics, which is a branch of mathematics dealing with data collection, analysis, interpretation, and presentation. Students will learn that the median is the middle value in a list of numbers, which provides a significant measure of the central tendency of the data. Emphasize the practicality of statistics in everyday life, such as determining the most common shoe size sold in a store or the average height in a class. Teach the steps to find the median: arranging numbers in order and finding the middle value. Conclude with an activity where students practice finding the median with various datasets to solidify their understanding.

Understanding the Median – Median: The middle number – Sort numbers and find the one in the middle – Steps to find the Median – 1. Arrange numbers 2. Locate middle number 3. If two middles, find their average – Example with a small dataset – Given 3, 7, 2, 6, sort to 2, 3, 6, 7. Median is (3+6)/2 = 4.5 | The median is a statistical measure that determines the middle value of a dataset when arranged in order. To find the median, students should first sort the numbers from smallest to largest. If there is an odd number of values, the median is the middle one. If there is an even number of values, the median is the average of the two middle numbers. Use the example provided to illustrate the process step by step. Encourage students to practice with different datasets to become comfortable with finding the median. This concept is fundamental in understanding data distribution and central tendency in statistics.

Sorting Numbers to Find the Median – Sorting numbers is the first step – Arrange numbers from smallest to largest – Practice sorting numbers as a class – We’ll sort a set of numbers together to understand – Activity: Sort numbers on the board – Each student will come up and sort a number | This slide introduces the concept of sorting numbers, which is essential in finding the median. Begin by explaining that the median is the middle number in a sorted list. Emphasize the importance of arranging numbers in order, either from smallest to largest or vice versa. During the activity, have each student participate by placing a number on the board in the correct order. This interactive approach helps students understand the process of sorting and prepares them for finding the median. Possible variations of the activity could include sorting numbers in small groups, using number cards, or interactive digital tools that simulate sorting. The goal is to ensure that every student grasps the concept of sorting as a precursor to finding the median.

Finding the Median: The Middle Value – Sort numbers from smallest to largest – Median is the middle for odd data sets – If 5 numbers, the 3rd is the median – For even sets, average the two middle numbers – With 6 numbers, average the 3rd and 4th – Practice finding the median with examples – Use sample data to calculate the median | This slide introduces the concept of finding the median in a data set. Start by explaining the importance of arranging the numbers in order, as this is a crucial step in determining the median. For an odd number of data points, the median will be the exact middle number. For an even number of data points, students will learn to find the average of the two middle numbers. Provide examples with both odd and even numbers of data points for the students to practice. Emphasize that the median is a type of average that can give us a sense of the ‘middle’ of a data set, which is particularly useful in understanding the distribution of numbers.

Median: Finding the Missing Number – Understanding the concept of Median – Median is the middle value in an ordered list – The role of Median with missing numbers – If a number is missing, the Median can help us find it – Steps to find the missing number – Order numbers, find the middle, use Median to calculate missing – Example: Solving with a known Median – Given list: 3, ?, 7, 9 with Median 6, find ? | This slide introduces the concept of finding a missing number in a sequence when the median is known. Start by explaining what a median is: the middle number in an ordered list of numbers. Emphasize that if the list is even, the median is the average of the two middle numbers. Then, explain how knowing the median can help us deduce the missing number in a sequence. Provide a step-by-step approach: arrange the numbers in order, locate the median’s position, and use it to figure out the missing number. Use the example provided to illustrate the process. Have students practice with additional problems where they have to find the missing number using the median.

Let’s Practice Together: Finding the Median – Class activity: Solve for the missing number – Work in pairs for problem-solving – Share your solutions with the class – Discuss how you found the median – Explain steps taken to determine the median in your set | This slide introduces a collaborative class activity focused on finding the missing number in a set to determine the median. Students are encouraged to work in pairs to foster teamwork and peer learning. After solving the problems, each pair will share their solutions with the class, explaining the process they used to find the median. As a teacher, prepare several sets of numbers with one number missing and ensure the sets are of varying difficulty to cater to different skill levels. Encourage students to arrange the numbers in order, identify the middle value, and use logical reasoning to find the missing number. Possible activities could include sets with even and odd numbers of terms, and scenarios where the median is one of the given numbers or needs to be calculated. This exercise will help students understand the concept of median in a practical and engaging way.

Real-Life Applications of Median – Median in daily life – Median is used to understand data like test scores, ages, and incomes. – Decision making with Median – Knowing the median can help choose better options when comparing. – Example: Median household income – The middle value of all the household incomes in a neighborhood. – Example: Median age – The age in the middle of a group can show the most common age range. | This slide aims to show students how the concept of median is not just a mathematical tool but a practical one that they encounter in various aspects of daily life. Understanding the median can help in making informed decisions, such as determining what is typical or common within a set of data. For instance, knowing the median household income of an area can help in understanding economic status, while the median age can indicate the demographics of a population. Encourage students to think of other examples where median might be useful and discuss how it can influence everyday choices.

Class Activity: Median Hunt – Find data in classroom or school – Look for numbers like book pages, locker numbers, or ages – Work in groups to calculate Median – Use the steps we learned to find the middle value – Present findings to the class – Share what you found and how you calculated the Median | This activity is designed to help students apply their knowledge of finding the median in a practical and engaging way. Divide the class into small groups and assign each group to collect a set of data from around the classroom or school, such as the number of pages in different books, locker numbers, or ages of students in a grade. Once they have their data, guide them to arrange the numbers in order and find the median. After calculating, each group will present their data set, the median they found, and the method they used to the rest of the class. This will reinforce their understanding of the concept of median and allow them to practice their presentation skills. Possible variations of data collection could include the number of leaves on plants, the length of pencils, or the number of chairs in each room.

Conclusion & Review: Understanding the Median – Recap: Median is the middle value – When numbers are in order, median is the middle one – Importance: Median shows the center – Median helps compare sets of data – Median calculation practice – Find the missing number to complete the set – Quick quiz on today’s lesson – Test your knowledge with a few questions | Today, we’ve learned that the median is the middle number in a sorted list of numbers, which helps us understand the central tendency of a data set. Knowing how to find the median is crucial because it’s less affected by outliers and skewed data compared to the mean. To ensure students have grasped the concept, we’ll end with a quick quiz covering how to find the median, especially when a number is missing in a sequence. This will reinforce their understanding and ability to apply the concept to various problems.