Your next great Lessn starts here.

Exploring Surface Area – What is Surface Area? – Total area of all faces and sides of a 3D object – Significance of Surface Area – Essential for material quantities, packaging, and design – Surface Area in Daily Life – From painting walls to wrapping gifts, it’s everywhere – Calculating Surface Area – Use formulas for cubes, prisms, and pyramids | This slide introduces the concept of surface area and its relevance in both mathematical theory and practical applications. Surface area is the sum of the areas of all the shapes that cover the surface of an object. Understanding this concept is crucial for students as it applies to various real-world scenarios such as construction, arts, and manufacturing. Emphasize the importance of surface area in determining the amount of material needed for a project or the amount of paint required to cover a surface. Provide examples like calculating the wrapping paper for a gift or the fabric needed for a tent. Encourage students to think of other examples where they might need to calculate surface area. Conclude with an overview of the formulas for finding the surface area of common shapes like cubes, prisms, and pyramids, setting the stage for more in-depth exploration in subsequent slides.

Surface Area of Cubes – Understanding a Cube – A cube is a 3D shape with 6 equal square faces. – Surface Area Formula: 6 * side^2 – To find the total surface area, multiply the area of one face by 6. – Example: Cube Surface Area Calculation – If a cube’s side is 3 cm, surface area = 6 * (3 cm)^2 = 54 cm^2. | This slide introduces the concept of a cube and how to calculate its surface area, which is a key topic in understanding three-dimensional shapes in geometry. Start by explaining that a cube is a special type of prism where all faces are equal squares. Emphasize that the formula for the surface area of a cube is derived from calculating the area of one face (side squared) and then multiplying by the total number of faces (6). Provide an example with a specific side length to demonstrate the calculation process. Encourage students to visualize the cube and its six equal faces to understand why the formula includes multiplying by 6. This will help solidify their understanding of surface area in relation to three-dimensional shapes.

Surface Area of Rectangular Prisms – Define a rectangular prism – A 3D object with 6 rectangular faces – Surface area formula: 2lw + 2lh + 2wh – l=length, w=width, h=height of the prism – Walkthrough: Calculating surface area – Example: Find surface area for l=3cm, w=4cm, h=5cm – Practice problem for students | Introduce the concept of a rectangular prism by describing its properties, such as having six faces, all of which are rectangles. Explain that the surface area is the total area of all the faces combined. Present the formula for calculating the surface area of a rectangular prism and ensure students understand each variable represents a dimension of the prism. Walk through an example calculation step-by-step, showing how to plug values into the formula. Finally, provide a practice problem for students to solve, reinforcing the concept. Encourage students to visualize the prism and its dimensions as they apply the formula.

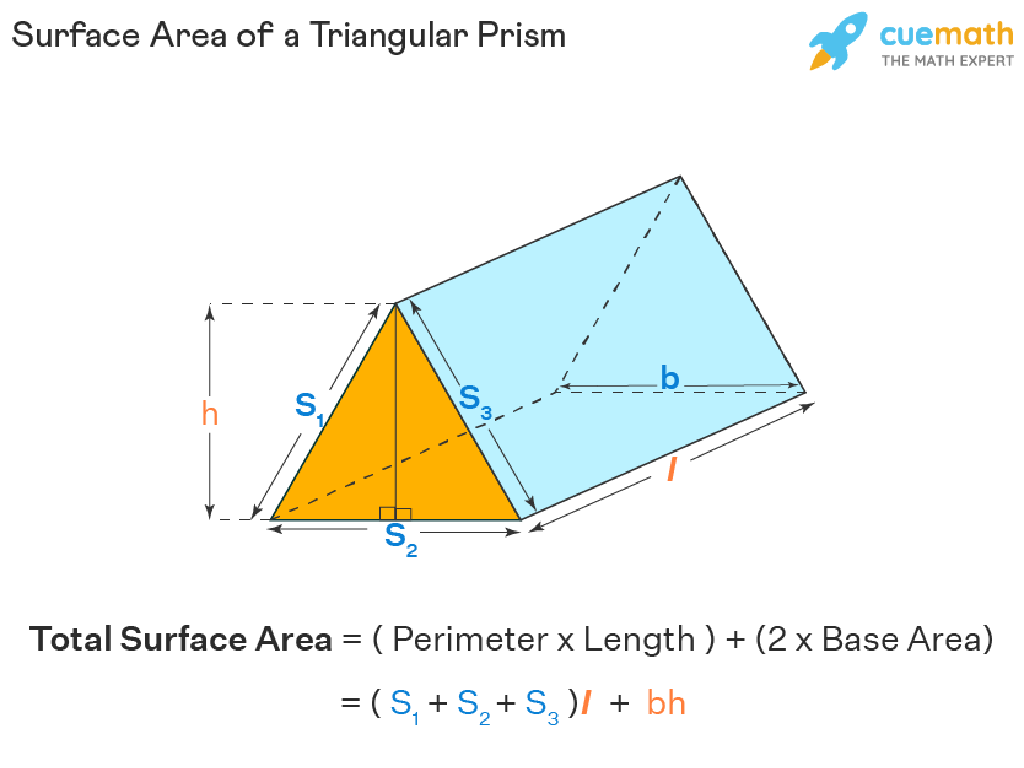
Surface Area of Triangular Prisms – What is a triangular prism? – A prism with triangular bases – Surface area formula: bh + 2ls + lw – ‘bh’ is base area, ‘ls’ is lateral surface, ‘lw’ is length*width – Step-by-step example calculation – We’ll calculate the surface area of a given prism together – Practice problem for students – Find the surface area of a prism with given dimensions | This slide introduces students to the concept of surface area for triangular prisms. Begin by identifying the shape and its characteristics, such as having two triangular bases and three rectangular faces. Explain the formula for surface area, where ‘bh’ represents the area of one triangular base, ‘2ls’ is the sum of the areas of the lateral faces, and ‘lw’ is the product of the length and width of the base. Walk through a detailed example, calculating the surface area step by step. Conclude with a practice problem, providing the dimensions of a triangular prism and asking students to calculate the surface area. This exercise will reinforce their understanding and application of the formula.

Surface Area of Pyramids – What is a pyramid? A pyramid has a base and triangular sides that meet at a point. – Surface area formula Surface area = Base area + 1/2 * Perimeter * Slant height – Example: Calculate surface area Find the surface area of a pyramid with a square base of side 4 cm and slant height 6 cm. – Practice problem | This slide introduces students to the concept of a pyramid in geometry, which is a solid with a base connected to triangular faces that converge at a single point. Emphasize the parts of a pyramid: base, face, vertex, and slant height. The formula for the surface area of a pyramid is explained, and students are shown how to apply it with an example. The base area is calculated depending on the shape of the base (square, rectangular, etc.), and the lateral surface area is found using the perimeter of the base and the slant height. Provide a practice problem for students to solve, reinforcing the concept. Encourage students to visualize the pyramid and its net to better understand the surface area calculation.

Practice Problems: Surface Area – Apply learned concepts – Collaborative problem-solving – Work through examples as a class to reinforce understanding – Individual practice encouraged – Students attempt problems independently to test skills – Review and discuss solutions – Discuss solutions as a class to ensure comprehension | This slide is designed to transition students from learning to application through practice problems. Start by revisiting the key concepts of calculating the surface area for cubes, prisms, and pyramids. Then, solve a few problems as a class to demonstrate the process. Next, provide students with a set of problems to work on individually, which will help them to internalize the methods. Finally, come back together as a class to review the solutions, allowing students to ask questions and clarify any misunderstandings. This approach ensures that students are not only able to follow along but also to apply the concepts independently.

Class Activity: Crafting 3D Shapes – Gather materials: paper, scissors, tape/glue – Construct cubes, prisms, and pyramids – Calculate surface area of each shape Use formulas: Cube (6a^2), Prism (2lw + 2lh + 2wh), Pyramid (a^2 + 2ab) – Reflect on the activity and findings Discuss challenges and insights gained | This hands-on activity is designed to help students understand the concept of surface area through a practical exercise. Provide students with paper, scissors, and tape or glue to construct basic 3D shapes such as cubes, prisms, and pyramids. Once constructed, guide them to calculate the surface area of each shape using the appropriate formulas. For a cube with side length ‘a’, the surface area is 6 times the area of one face (6a^2). For a prism with length ‘l’, width ‘w’, and height ‘h’, the surface area is the sum of the areas of all faces (2lw + 2lh + 2wh). For a pyramid with base area ‘a’ and slant height ‘b’, the surface area includes the base area plus half the perimeter times the slant height (a^2 + 2ab). After the activity, encourage students to share their experiences, any difficulties they encountered, and what they learned about surface area.

Surface Area Review & Q&A – Recap surface area concepts Surface area is the total area of all faces of a 3D shape. – Ask your questions now – Let’s clarify your doubts – Ensure understanding for all We’ll review examples to solidify comprehension. | This slide is aimed at reviewing the key concepts of calculating the surface area for cubes, prisms, and pyramids. Start by summarizing the methods used to find the surface area of each shape. Encourage students to ask any questions they have about the topic, and be prepared to clarify doubts with additional examples or explanations. The goal is to ensure that all students have a solid understanding of the surface area before moving on to more complex topics. Consider having a few practice problems ready to go through as a class to demonstrate common misunderstandings and how to avoid them.

Homework: Mastering Surface Area – Complete the worksheet provided – Practice calculating surface area – Find the total area of each face and sum up – Review formulas for cubes, prisms, pyramids – Remember: Area of cube = 6a^2, Prism = 2B + Ph, Pyramid = B + 1/2Pl – Get ready for the next class quiz | This homework assignment is designed to reinforce the concepts taught in class about the surface area of various shapes. The worksheet will provide a variety of problems that require students to apply formulas and calculate the surface area of cubes, prisms, and pyramids. Encourage students to review their class notes and textbook examples to prepare for the quiz. Remind them that understanding these concepts is not only crucial for the quiz but also for real-world applications such as packaging design and architecture. Provide tips on how to approach each problem and remind them to check their work for accuracy.