Your next great Lessn starts here.

Exploring Surface Area of Cylinders – Understanding Surface Area – Surface area is the total area of all the shapes that cover the surface of an object. – Surface Area in Daily Life – Used in engineering, design, and packaging. Think paint needed for a pipe. – Focusing on Cylinders – A cylinder has curved and flat surfaces; we’ll learn how to calculate both. – Preview of Today’s Lesson | Begin the lesson by explaining the concept of surface area as the sum of all areas that cover the surface of a 3D object. Highlight the practical applications of understanding surface area, such as in determining the amount of material needed for construction or manufacturing. Introduce cylinders as a common shape encountered in real life, from cans to pipes, and emphasize the importance of calculating their surface area. Provide a brief overview of what the lesson will entail, including the formulas and methods for finding the surface area of cylinders, to prepare students for the detailed exploration to come.

Exploring Cylinders: Surface Area and Volume – Define a cylinder – A 3D shape with two parallel circular bases and a curved side – Identify cylinder parts – Base: circular top and bottom, Lateral Surface: curved side, Height: distance between bases – Everyday life cylinder examples – Cans, pipes, and drums are common cylindrical objects – Calculate surface area – Use formula 2Àr(h + r) to find total surface area | This slide introduces students to the concept of a cylinder, a fundamental three-dimensional shape in geometry. Start by defining a cylinder and discussing its parts: the base, lateral surface, and height. Use tangible examples like cans, pipes, and drums to help students identify cylinders in everyday life. Emphasize the role of the radius (r) and height (h) in calculating the surface area. The formula for the surface area of a cylinder is 2Àr(h + r), where À is approximately 3.14. Encourage students to visualize how the lateral surface can be ‘unrolled’ into a rectangle to understand how the formula is derived. Provide practice problems for students to apply the formula and calculate the surface area of various cylinders.

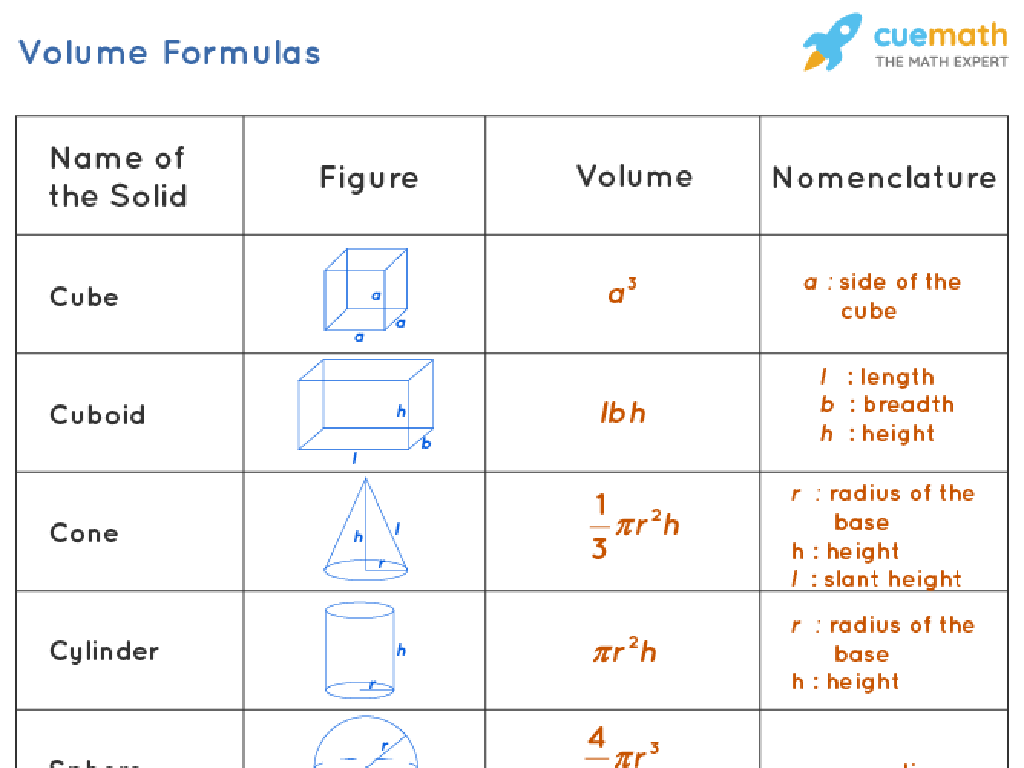
Calculating the Surface Area of Cylinders – Surface area formula for cylinders – 2Àrh + 2Àr^2, where r is radius and h is height – Lateral area and base areas – Lateral area: 2Àrh, area of the bases: 2Àr^2 – The role of Pi (À) in the formula – Pi (À) represents the ratio of circumference to diameter of a circle – Practical examples using the formula – Calculate surface area of a can or a pipe | This slide introduces the mathematical formula for calculating the surface area of a cylinder, which is an essential concept in geometry. The formula is broken down into two parts: the lateral area (the side surface of the cylinder) and the area of the bases (the top and bottom circles). Pi (À) is a crucial part of the formula, and it’s important for students to understand its significance as the constant ratio in all circles. Provide practical examples such as finding the surface area of everyday cylindrical objects like cans or pipes to help students visualize and apply the formula. Encourage students to practice by measuring and calculating the surface area of various cylinders they encounter in their daily lives.

Calculating Lateral Surface Area of Cylinders – Lateral Surface Area formula – Use LSA = 2Àrh, where r is radius and h is height – Example: Calculate with given r and h – If r=3cm, h=5cm, LSA = 2À(3)(5) = 30À cm² – Practice Problem for you – Try finding LSA with r=4cm, h=7cm | This slide introduces the concept of Lateral Surface Area (LSA) for cylinders, which is the area of the sides of the cylinder without the top and bottom. The formula LSA = 2Àrh is crucial and students should memorize it. The example provided uses specific values for the radius (r) and height (h) to demonstrate how to apply the formula. For the practice problem, students are given different values for r and h to calculate the LSA on their own. This exercise will help solidify their understanding of the concept and the application of the formula. Encourage students to show their work step by step and to check their answers with a partner.

Calculating the Surface Area of Cylinder Bases – Area of one base formula – Use Àr^2 to find the area of one circular base – Multiply by two for both bases – Since a cylinder has two bases, we double the area of one base – Total area of bases – Add the areas of both bases to find the total area – Practice with an example – Find the area of bases for a cylinder with radius 3 cm | This slide focuses on the initial step in calculating the surface area of a cylinder: finding the area of the bases. Start by explaining the formula for the area of a circle, Àr^2, where r is the radius. Emphasize that since a cylinder has two identical circular bases, students will need to calculate the area of one base and then multiply by two to find the total area of both bases. Provide a practice problem for students to apply this knowledge, such as calculating the total area of the bases for a cylinder with a given radius. This exercise will prepare them for understanding the complete surface area calculation of a cylinder.

Calculating Total Surface Area of Cylinders – Total Surface Area formula – Add lateral area and bases’ areas together – Walkthrough of an example – Example: Find TSA of a cylinder with h=5cm, r=3cm – Step-by-step guided practice – Follow along as we solve an example together – Apply formula to new problems | This slide aims to consolidate the students’ understanding of how to calculate the total surface area (TSA) of a cylinder. Begin by revisiting the formula for TSA, which is the sum of the lateral surface area and the areas of the two bases. Provide a full example, such as finding the TSA of a cylinder with a given height (h) and radius (r), and solve it together with the class. This will help students see the application of the formula in a practical context. Then, guide them through a practice problem, ensuring they understand each step of the process. Finally, encourage students to apply the formula to new problems, reinforcing their learning and building confidence in their ability to tackle similar questions independently.

Real-World Applications of Surface Area – Surface area in engineering – Engineers use surface area to determine material quantities and costs. – Packaging and surface area – Packaging efficiency depends on optimizing the surface area to volume ratio. – Interactive Q&A session – Significance of surface area – Surface area is crucial for material usage, cost, and practical design. | This slide aims to connect the mathematical concept of surface area with its practical applications in the real world. Discuss how engineers must calculate the surface area for projects, affecting the amount of material needed and the cost. Explore how companies make packaging decisions based on the surface area to minimize material use and maximize space. The interactive Q&A session will engage students in thinking critically about why surface area is a vital consideration in many aspects of design and manufacturing. Encourage students to think of examples where surface area plays a role in their daily lives, such as in sports equipment or furniture design.

Class Activity: Exploring Surface Area – Measure objects to find surface area – Group task: Make a surface area poster – Choose various cylindrical objects, measure them, and calculate their surface area. – Share your group’s findings – Present your calculations creatively on a poster. – Discuss the results as a class – Each group will explain their methods and results. | This interactive class activity is designed to help students apply their knowledge of calculating the surface area of cylinders to real-world objects. Students will work in groups to measure cylindrical objects found in the classroom, such as cans, jars, or tubes. They will then use the formula for surface area of a cylinder (2Àrh + 2Àr^2) to calculate the surface area of each object. Each group will create a poster displaying their objects, measurements, calculations, and any challenges they faced. Afterward, groups will share their posters with the class and discuss their findings, allowing students to see a variety of approaches and understand common mistakes. The teacher should circulate during the activity to provide guidance and ensure accuracy in measurements and calculations. Possible objects for measurement include a water bottle, a pencil holder, or a paper towel roll.

Homework: Mastering Cylinder Surface Area – Practice problems on cylinder surface area – Solve assigned problems to strengthen understanding – Explore surface areas around you – Measure and calculate surface area of cylinders at home or school – Reminder: Consistent practice is key – Share findings of real-world cylinders – Bring examples of cylinder surface areas you’ve found for class discussion | For homework, students are to complete a set of practice problems focusing on calculating the surface area of cylinders. This will help reinforce the day’s lesson and solidify their understanding. Additionally, students should look for cylindrical objects in their environment, such as cans or tubes, measure them, and calculate the surface area. This real-world application will make the concept more tangible. Remind students that becoming proficient at these calculations requires regular practice. In the next class, ask students to share their real-world findings, which will encourage engagement and provide a platform for discussing practical applications of mathematical concepts.

Wrapping Up: Surface Area of Cylinders – Recap of cylinder surface area Surface area = 2Àrh + 2Àr², where r is radius, h is height. – Significance of surface area Understanding this helps in real-life applications like packaging. – Open floor for questions – Encourage exploration at home Try calculating objects at home, like cans. | As we conclude today’s lesson on the surface area of cylinders, it’s important to revisit the key formula and its components. Emphasize the practicality of understanding surface area in various fields, such as engineering, design, and everyday life. Encourage students to ask questions if they’re unsure about any part of the lesson to ensure clarity and understanding. Additionally, motivate them to apply their knowledge by identifying cylindrical objects at home and calculating their surface area. This not only reinforces the lesson but also helps them see the relevance of math in the real world.