Your next great Lessn starts here.

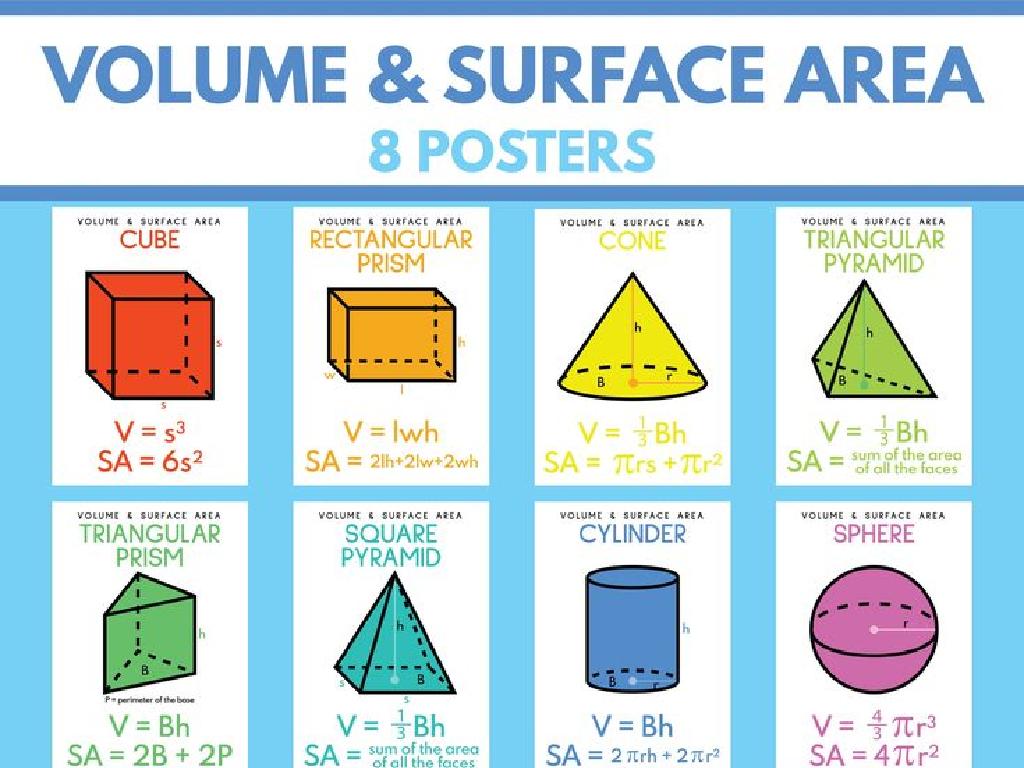
Exploring the Volume of Spheres – Understanding 3D shapes – Objects with length, width, and height – Defining volume – Space occupied by an object – Volume in everyday life – Balls, bubbles, and globes – Calculating sphere volume – Use formula 4/3Àr^3 for spheres | This slide introduces students to the concept of volume within three-dimensional shapes, focusing on spheres. Begin by discussing common 3D shapes and their properties, emphasizing that volume measures the space they occupy. Provide relatable examples such as sports balls, soap bubbles, and globes to illustrate volume in daily life. Conclude by presenting the formula for the volume of a sphere (4/3Àr^3) and explain each part of the formula. Encourage students to think of other spherical objects and consider their volume. This will set the foundation for more in-depth exploration of volume calculations in subsequent lessons.

Exploring Spheres: Understanding Volume – What is a sphere? – A sphere is a 3D object with all points equidistant from the center. – Key properties of spheres – Spheres have a smooth surface with no edges or vertices. – Spheres in the real world – Examples: basketballs, globes, bubbles. – Calculating sphere volume – Volume formula: V = 4/3Àr³, where r is the radius. | This slide introduces students to the concept of spheres, their properties, and their presence in everyday life. Begin by defining a sphere and discussing its uniformity in all directions. Highlight that unlike polyhedra, spheres have no flat surfaces or sharp corners. Provide tangible examples of spheres that students encounter, such as sports balls or soap bubbles, to illustrate the concept. Conclude with the mathematical formula for calculating the volume of a sphere, emphasizing the importance of À and the radius in this calculation. Encourage students to visualize filling a sphere with unit cubes to understand volume conceptually. Provide practice problems involving spheres of different sizes to solidify their understanding.

Volume of a Sphere – Sphere volume formula V = 4/3 Àr³ – Grasping the volume formula – Understand how the formula is derived and its geometric meaning. – Significance of À in the formula – À (pi) is a constant representing the ratio of circumference to diameter of a circle. – Role of radius (r) in volume – Radius (r) is the distance from the center to the surface; it’s crucial in determining size. | This slide introduces the mathematical concept of calculating the volume of a sphere, which is a crucial topic in geometry. The formula V = 4/3 Àr³ encapsulates the relationship between the volume of a sphere and its radius. It’s important for students to understand each component of the formula: ‘V’ stands for volume, ‘À’ is approximately 3.14159 and represents the constant relationship in all circles, and ‘r’ is the radius of the sphere. Emphasize the power of three on the radius, indicating that volume is a cubic measurement. Provide examples with different radii to illustrate how changes in radius affect the volume exponentially. Encourage students to memorize the formula and practice with various exercises to strengthen their understanding.

Calculating the Volume of a Sphere – Volume formula for a sphere – V = 4/3 Àr³, where r is radius – Example with a 5 cm radius – For r = 5 cm, what’s the volume? – Step-by-step calculation – Calculate volume: V = 4/3 À(5)³ – Units in volume calculation – Always include cubic units, cm³ | This slide is aimed at teaching students how to calculate the volume of a sphere. Start by explaining the formula V = 4/3 Àr³, where ‘V’ stands for volume and ‘r’ is the radius of the sphere. Use a specific example with a radius of 5 cm to show how to apply the formula. Walk through the calculation step by step, plugging the radius into the formula, and emphasize the importance of cubed units (cm³) to express volume. This will help students understand that volume is a measure of three-dimensional space. Encourage students to practice with spheres of different sizes and to always pay attention to units when calculating volume.

Volume of Spheres: Practice Problems – Calculate volume with given radius – Use formula V = 4/3 Àr³ for a sphere with radius r – Find radius from known volume – Rearrange formula to r = (3V/4À)^(1/3) for volume V – Solve a real-life volume problem – Apply volume calculation to a real-world scenario, like determining how much water a spherical tank can hold | This slide presents three practice problems to reinforce the concept of calculating the volume of spheres. The first problem focuses on using the standard volume formula when the radius is known. The second problem challenges students to work backwards from a given volume to find the sphere’s radius, requiring them to manipulate the volume formula. The third problem encourages students to apply their knowledge to a practical situation, which helps in understanding the relevance of the concept in real life. For the activity, consider having different problems for different groups, such as varying the known values or the context of the real-life application, to cater to different learning paces and to keep the activity engaging.

Class Activity – Let’s Measure: Volume of Spheres – Measure spherical objects – Calculate volume using formula Use formula V = 4/3 Àr^3, where r is the radius – Work in small groups – Share findings with class | This activity is designed to provide hands-on experience with measuring and calculating the volume of spheres. Provide a variety of spherical objects for students to measure, such as balls and globes. Distribute measuring tapes to each group and ensure they understand how to measure the circumference to find the radius. Once they have the radius, guide them to apply the volume formula V = 4/3 Àr^3. Have each group calculate the volume of their assigned objects, then share and compare their results with the class. Possible variations of the activity could include comparing volumes of different objects, estimating volume before measuring, or graphing the relationship between circumference and volume.

Review and Q&A: Volume of Spheres – Recap: Volume of a sphere formula – V = 4/3 Àr³, where V is volume and r is radius – Ask your questions about spheres – Let’s clarify doubts together – Any confusion over the formula or examples? – Addressing common misconceptions – Common errors include confusing radius with diameter | This slide is aimed at reviewing the formula for calculating the volume of spheres and providing a platform for students to ask questions and clarify any doubts. Begin with a quick recap of the formula, V = 4/3 Àr³, and ensure students remember how to apply it. Open the floor for students to ask any questions they might have about the volume of spheres, encouraging participation. Address any doubts that arise, ensuring that students understand the concept clearly. Pay special attention to common misconceptions, such as confusing the radius with the diameter, and provide additional examples if necessary to solidify understanding. The goal is to ensure that all students leave the class with a firm grasp of how to calculate the volume of spheres.

Homework: Exploring Sphere Volumes – Complete the sphere volume worksheet – Measure spherical objects at home – Find objects like balls or oranges and use a measuring tape – Record your findings – Write down the object’s measurements and calculate the volume – Remember, practice is key! | This homework assignment is designed to reinforce the concept of volume calculation for spheres. Provide students with a worksheet that includes a variety of problems, ranging from simple to complex, to solve for the volume of spheres. Encourage students to apply their knowledge practically by finding spherical objects around their home, such as a basketball or an orange, and measure their circumference to calculate the volume. Remind them that accuracy in measurement is crucial. Emphasize the importance of practice in mastering mathematical concepts and encourage them to solve additional problems if they finish early. For the next class, plan to review the homework answers and discuss any challenges students faced.