Your next great Lessn starts here.

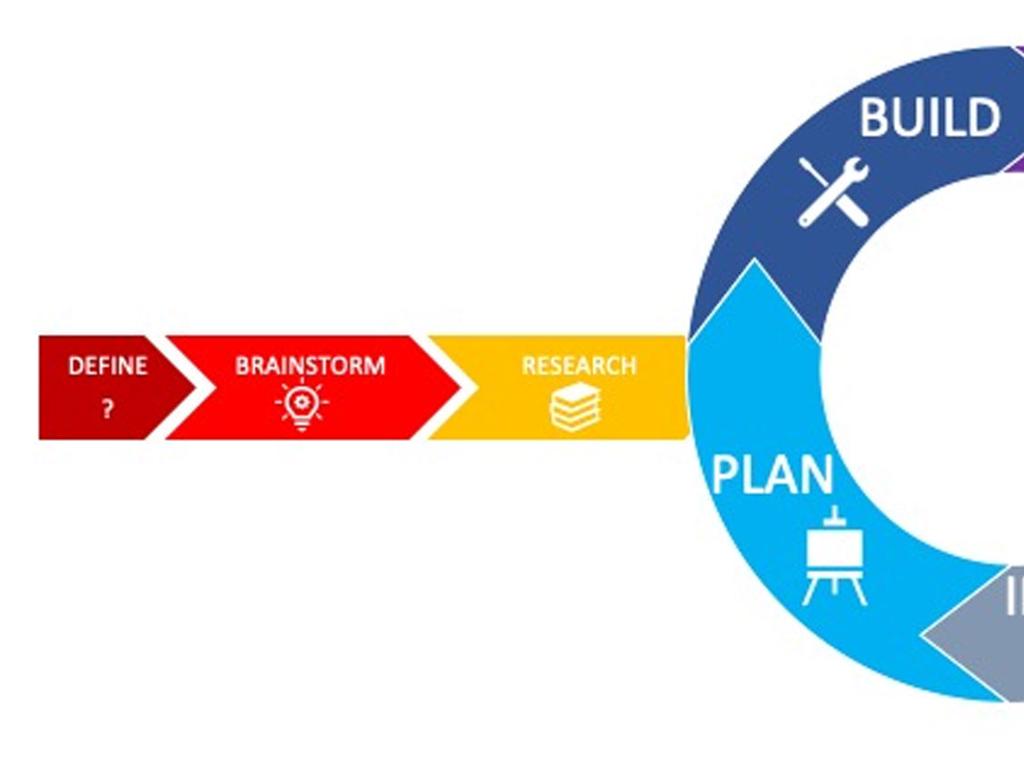
Solving Systems of Equations in Real Life – Define systems of equations – A set of two or more equations with the same variables – Real-world application examples – Budgeting, mixing solutions, or planning trips – Overview of solving methods – Graphing, substitution, elimination – Emphasize practical relevance | This slide introduces students to the concept of systems of equations, which are fundamental in solving real-world problems involving multiple variables. Begin by defining a system of equations and explaining that they consist of two or more equations that share the same variables. Provide relatable examples such as budgeting money, determining the right mix of chemicals in a solution, or planning a trip to illustrate how these systems appear in everyday life. Briefly overview the methods of solving these systems, including graphing, substitution, and elimination, and discuss when each method might be most effective. Emphasize the importance of understanding these concepts for practical problem-solving in various fields such as science, engineering, and economics. Encourage students to think of other areas where systems of equations might be applied.

Understanding Systems of Equations – Define system of equations – A set of two or more equations with the same variables – Types: consistent, inconsistent, dependent – Consistent: one solution, Inconsistent: no solution, Dependent: infinitely many solutions – Visualizing system types – Graphs intersect (consistent), are parallel (inconsistent), or are the same line (dependent) – Solving word problems | Introduce the concept of a system of equations as a foundational element in algebra, emphasizing that it consists of multiple equations that share variables. Explain the three types of systems: consistent systems have a single solution where the graphs of the equations intersect at a point; inconsistent systems have no solution as the equations represent parallel lines that never intersect; dependent systems have infinitely many solutions because the equations represent the same line. Use visual aids to help students differentiate between these types by showing examples of each on a graph. Conclude with an introduction to applying these concepts to solve word problems, which will be covered in more detail in subsequent slides. Encourage students to think of real-life situations that could be modeled with a system of equations.

Solving Systems of Equations: Word Problems – Graphical method overview – Plot equations on a graph and find the intersection point. – Substitution method explained – Replace one variable with its equivalent from the other equation. – Elimination method steps – Add or subtract equations to eliminate one variable. – Choosing the best method | This slide introduces students to the three primary methods for solving systems of equations in the context of word problems. The graphical method involves plotting both equations on a graph and finding the point where they intersect, which represents the solution. The substitution method requires solving one equation for one variable and substituting this into the other equation. The elimination method involves adding or subtracting the equations to cancel out one of the variables, making it possible to solve for the other. Encourage students to understand each method’s process and to practice deciding which method is most efficient for different types of problems. Provide examples of word problems and guide students through the process of solving them using each method.

Solving Systems of Equations: Word Problems – Comprehend word problems – Identify variables and equations – Variables represent unknowns, equations model the problem – Formulate a system of equations – Translate the problem’s story into mathematical expressions – Solve the system step by step – Use methods like substitution or elimination to find solutions | This slide introduces students to the process of solving word problems involving systems of equations. Start by ensuring students understand the context and details of the word problem. Next, guide them to identify the unknown quantities which will be represented as variables. Show them how to derive equations based on the relationships described in the problem. Once the system of equations is set up, walk them through solving it using a method they are comfortable with, such as substitution or elimination. Emphasize the importance of checking their solutions in the context of the original problem to ensure they make sense. Provide examples and practice problems to solidify their understanding.

Solving Systems of Equations: Word Problems – Read the problem as a class – Determine the unknowns – Identify variables that represent unknown quantities – Translate to a system of equations – Use key phrases to form equations representing the relationships – Solve the system step by step – Apply methods like substitution or elimination to find solutions | This slide is aimed at guiding students through the process of solving word problems by forming and solving a system of equations. Start by reading the problem aloud to ensure comprehension. Next, help students identify the unknowns, which will become the variables in the equations. Teach them to look for phrases that indicate mathematical operations and relationships to translate the word problem into algebraic expressions. Finally, demonstrate how to solve the system using a chosen method, such as substitution or elimination, and check the solution by plugging it back into the original equations. Encourage students to work through the problem in a step-by-step manner and to collaborate with peers if they encounter difficulties.

Solving Systems of Equations: Word Problems – Selecting the right method – Compare substitution, elimination, and graphing methods – Step-by-step problem solving – Follow algebraic steps to find variable values – Understanding the solution – What do the variable values represent? – Relating solution to the problem – Apply the answer back to the real-world scenario | This slide is aimed at guiding students through the process of solving a system of equations presented in a word problem. Start by discussing how to choose the most efficient method (substitution, elimination, or graphing) based on the given equations. Then, demonstrate solving the system step by step, ensuring to show each algebraic manipulation clearly. Once the solution is found, explain how to interpret the values of the variables in the context of the problem, emphasizing the importance of understanding what the solution actually means in real life. Finally, relate the solution back to the original word problem to illustrate how math can be used to solve practical problems. Encourage students to ask questions if they’re unsure about any step.

Solving Systems of Equations: Word Problems – Work through new word problems – Set up systems of equations – Translate problems into equations with variables representing unknowns – Solve the systems step-by-step – Use substitution, elimination, or graphing to find solutions – Discuss solutions and methods – Share different approaches and understand various methods | This slide is aimed at providing students with practice on solving systems of equations through word problems. Students should work independently to translate word problems into algebraic equations, representing unknowns with variables. They should then attempt to solve these systems using their preferred method, whether it be substitution, elimination, or graphing. After solving, students will engage in a class discussion to compare solutions and the different methods used, fostering a deeper understanding of the concepts and encouraging collaborative learning. The teacher should facilitate the discussion, ensuring that each student understands the process and can articulate their reasoning.

Class Activity: Solve & Share – Pair up and solve a word problem – Present your problem and solution – Explain the method used – Did you use substitution, elimination, or graphing? – Engage in class feedback session – Discuss the merits of different methods | This activity is designed to foster collaborative problem-solving and presentation skills. Students will work in pairs to tackle a system of equations word problem, using any method they prefer (substitution, elimination, or graphing). After solving, they will present their problem, the solution they found, and the method they used to the class. This will be followed by a feedback session where students can discuss the different approaches taken by their peers. As a teacher, facilitate the discussion to ensure that each method’s strengths and weaknesses are explored. Encourage students to ask questions and provide constructive feedback. Possible activities for different pairs could include solving for the number of items at different prices, mixing solutions with different concentrations, or finding the intersection point of two lines representing different situations.

Review & Practice: Systems of Equations – Recap key concepts – Review solving systems by graphing, substitution, and elimination. – Address common challenges – Discuss issues like variable isolation or incorrect graphing. – Homework assignment – Tips for successful problem-solving – Practice makes perfect. Use the homework to apply what you’ve learned. | This slide aims to consolidate the students’ knowledge on solving systems of equations. Begin with a brief review of the methods taught: graphing, substitution, and elimination. Highlight the importance of finding the point of intersection in graphing, the need for accurate variable isolation in substitution, and the correct setup for elimination. Address common issues students may face, such as difficulties with algebraic manipulation or plotting points accurately. Assign homework that covers a range of problems, ensuring there are examples that require each method. Encourage students to approach challenges as opportunities to learn, and remind them that practice is key to mastery. Provide strategies for checking their work, such as plugging solutions back into the original equations.