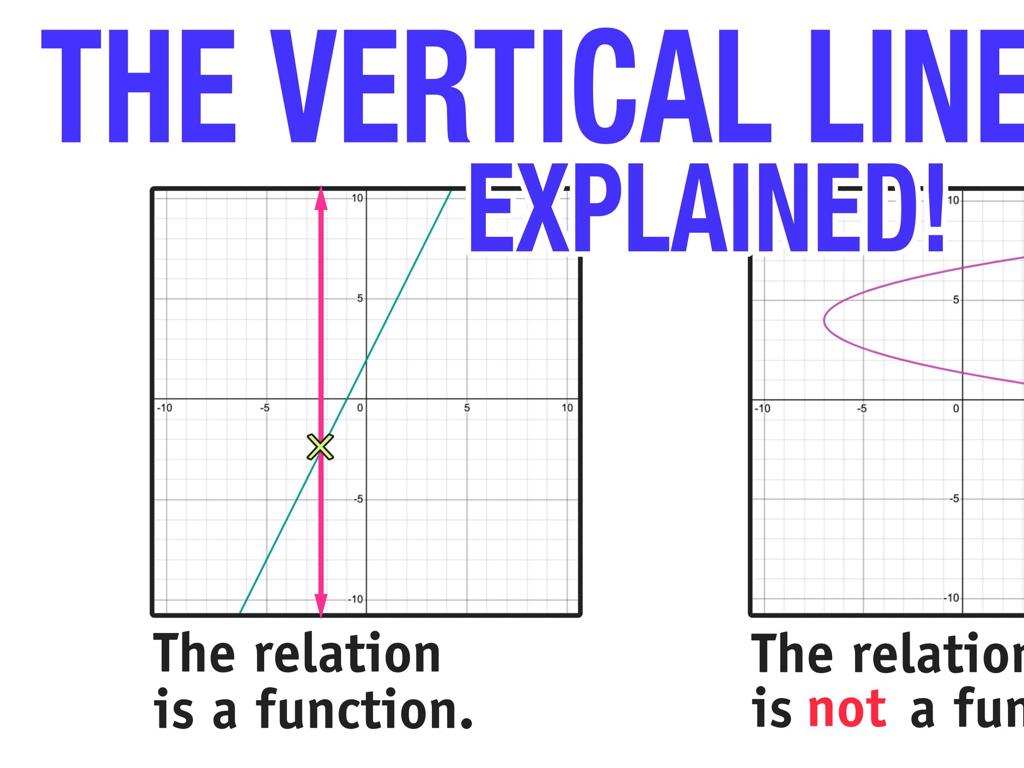
Reflections: Find The Coordinates
Subject: Math
Grade: Eighth grade
Topic: Transformations And Congruence
Please LOG IN to download the presentation. Access is available to registered users only.
View More Content
Reflections: Finding the Coordinates
– Understanding mathematical transformations
– Transformations include operations like reflections, rotations, and translations.
– Defining congruence in geometry
– Congruence means two shapes are identical in shape and size, but may be flipped or rotated.
– Exploring reflections in the coordinate plane
– Reflections flip a shape over a line, creating a mirror image.
– How to find coordinates after reflection
– Use the formula (x, y) (-x, y) for reflection over the y-axis, and (x, y) (x, -y) for the x-axis.
|
This slide introduces the concept of transformations and congruence, with a focus on reflections. Transformations are operations that alter the position of figures in the coordinate plane, while congruence deals with figures being identical in shape and size. Reflections are a type of transformation that create a mirror image of a shape across a line called the axis of reflection. When reflecting a point across the y-axis, the x-coordinate changes sign; when reflecting across the x-axis, the y-coordinate changes sign. Provide examples on the board and encourage students to practice reflecting points and shapes to solidify their understanding.
Understanding Reflections in Geometry
– Define geometric reflection
– A flip over a line where the figure is the same distance from the line on both sides.
– Reflections create mirror images
– Like looking in a mirror, points are reversed across a line to create a mirror image.
– Explore properties of symmetry
– Reflective symmetry means each point of an image is the same distance from the line as its counterpart.
– Reflections across the x and y-axis
– When reflecting over the x-axis or y-axis, the coordinates change in a specific way.
|
This slide introduces the concept of reflection in geometry, which is akin to looking in a mirror. Each point of the original shape appears at an equal distance on the opposite side of a given line, known as the line of reflection. Emphasize that reflective symmetry is a fundamental property where each point and its reflected counterpart are equidistant from the line of reflection. When reflecting over the x-axis, the y-coordinate changes sign, and when reflecting over the y-axis, the x-coordinate changes sign. Provide examples of reflections across both axes and encourage students to practice with coordinate plotting to solidify their understanding.
Coordinates and The Coordinate Plane
– Recap on coordinates
– Coordinates are a set of values that show an exact position.
– Understanding X and Y axes
– X-axis is horizontal, Y-axis is vertical.
– How to plot points
– Use ordered pairs (x, y) to locate points.
– Reflections and coordinates
– Reflecting a point across an axis changes its coordinates.
|
Begin with a brief review of what coordinates are and how they are used to indicate positions on a plane. Ensure students understand the layout of the coordinate plane, including the horizontal X-axis and the vertical Y-axis. Demonstrate how to plot points using ordered pairs, where the first number corresponds to the X-axis and the second to the Y-axis. Discuss how reflections over either axis will alter the coordinates of a point, leading into the concept of finding the coordinates of a reflected point. Provide examples and encourage students to practice plotting and reflecting points to solidify their understanding.
Rules for Reflections in Coordinate Geometry
– Reflecting points across the X-axis
– To reflect a point across the X-axis, invert the Y-coordinate (e.g., (3, 4) becomes (3, -4))
– Reflecting points across the Y-axis
– To reflect a point across the Y-axis, invert the X-coordinate (e.g., (3, 4) becomes (-3, 4))
– Reflections across other lines
– Use the formula (x, y) -> (-x, -y) for reflection across the origin; other lines require different approaches
– Practical applications of reflections
|
This slide introduces the concept of reflections in coordinate geometry, a key component of understanding transformations and congruence. When reflecting a point across the X-axis, the Y-coordinate changes sign, while reflecting across the Y-axis changes the sign of the X-coordinate. For reflections across other lines, such as the line y = x or the origin, students will learn specific rules and formulas. Emphasize the importance of understanding these concepts not only for academic purposes but also for their practical applications in fields like computer graphics and physics. Provide examples on the board and encourage students to practice with coordinates to solidify their understanding.
Reflections in Action: Triangles
– Reflecting a triangle example
– Reflect triangle over x or y-axis and note changes
– How to find new coordinates
– New coordinates are opposite in sign to the axis of reflection
– Walkthrough of a practice problem
– Step-by-step solution to a reflection problem
– Understanding reflections in geometry
|
Begin with an example of reflecting a triangle across an axis, showing the original and reflected shapes. Explain that when reflecting over the x-axis, the y-coordinates change sign, and when reflecting over the y-axis, the x-coordinates change sign. Walk through a practice problem, reflecting a point or shape and finding the new coordinates. Emphasize the ‘mirror image’ concept in reflections and how coordinates change. This will help students visualize and understand the process of reflection in coordinate geometry. Encourage students to practice with additional problems to solidify their understanding.
Let’s Practice Reflections!
– Reflect shapes on graph paper
– Identify vertices post-reflection
– Note original and new coordinates
– Share results with a partner
– Explain how you found the new points
– Discuss reflection properties
|
This slide introduces a hands-on activity where students will practice the concept of reflection in geometry. Provide each student with graph paper and a set of shapes to reflect over a specified axis. After reflecting the shapes, students should identify and record the coordinates of the vertices of the reflected shape. Encourage them to compare the original and reflected coordinates to understand the properties of reflection. Once they have completed their reflections, students should pair up to share and discuss their results. This peer interaction will help solidify their understanding. As a teacher, circulate the room to assist and ask guiding questions. Possible activities for different students could include reflecting over the x-axis, y-axis, or a line like y=x, to show how reflections can vary depending on the ‘mirror’ line.
Reflections in the Real World
– Reflections around us
– Mirrors, water bodies, and windows
– Daily applications of reflections
– Used in designing periscopes, kaleidoscopes, and in art
– Significance of understanding reflections
– Grasping the concept aids in fields like physics, engineering, and architecture
|
This slide aims to connect the mathematical concept of reflections with real-world applications to make it more relatable for students. Begin by discussing how reflections are present in everyday life, such as in mirrors, calm bodies of water, or through windows. Highlight how reflections are used in various tools and devices like periscopes and kaleidoscopes, and their importance in artistic design. Emphasize the significance of understanding reflections for practical applications in fields such as physics, where light reflection principles are crucial, engineering for designing reflective surfaces, and architecture for creating symmetrical designs. Encourage students to think of other examples where reflections play a role and to consider the underlying geometry involved in these phenomena.
Class Activity: Coordinate Reflections
– Create your own geometric design
– Reflect your design across an axis
– Use the x or y-axis as your ‘mirror’ for reflection
– Determine coordinates of the reflection
– Apply reflection rules to find new coordinates
– Present both designs to the class
|
This activity is designed to help students understand the concept of reflection in the coordinate plane. Students will create a geometric design on graph paper, choose an axis to reflect over, and then apply the rules of reflection to find the coordinates of the reflected image. For example, reflecting over the y-axis changes the sign of the x-coordinates. After completing their reflections, students will present their original and reflected designs, explaining the process they used to find the coordinates. This will reinforce their understanding and allow for peer learning. Possible variations include reflecting over the x-axis, y-axis, or even the line y=x. Encourage creativity in their designs and ensure they label all points clearly.
Wrapping Up: Reflections and Looking Ahead
– Recap of reflection principles
– Remember, reflections flip coordinates over a line
– Homework: Reflection worksheet
– Practice finding reflected points on a grid
– Upcoming topic: Rotations
– Understanding rotations will build on reflection knowledge
– Importance of mastering reflections
|
As we conclude today’s lesson on reflections, remind students of the key concept: a reflection is a transformation that flips a figure over a line of reflection, changing the position of the figure while maintaining its shape and size. For homework, students should complete the provided worksheet, which will reinforce their ability to find the coordinates of reflected points. Looking ahead, we will explore rotations, another type of transformation in the coordinate plane. It’s crucial for students to grasp reflections well, as it will make understanding rotations easier. Encourage students to ask questions if they’re unsure about today’s material, and remind them that practice is key to mastering these concepts.

/colonial_america_settlement.jpg)