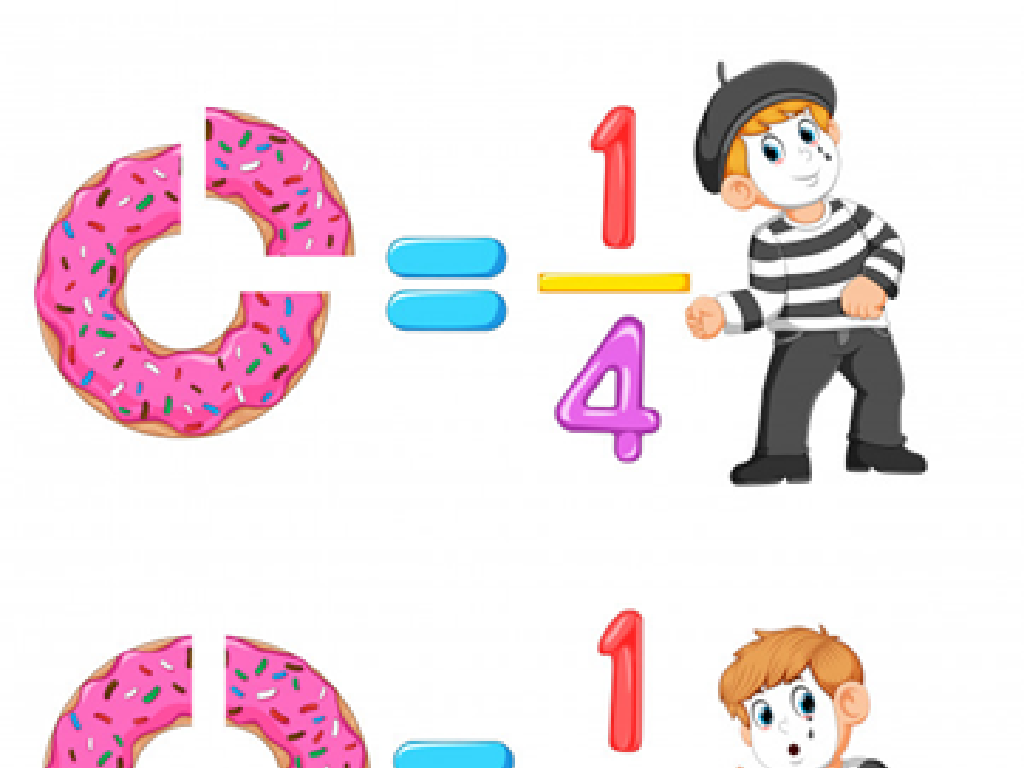Your next great Lessn starts here.

Welcome to Fraction Division! – Understanding fraction division – Today’s goal: Divide whole numbers by unit fractions – What is a unit fraction? – A unit fraction has 1 as the numerator, like 1/3 or 1/4. – Using models to divide – Visual aids like pie charts help us see how division works. | Today’s lesson introduces students to the concept of dividing whole numbers by unit fractions. Begin by explaining what fraction division is and how it differs from whole number division. Emphasize that our goal is to understand this concept using models, which will make it easier to visualize. Clarify that a unit fraction is a fraction with a numerator of 1. Use models such as pie charts or fraction bars to demonstrate how a whole number can be divided by a unit fraction, showing the division as the number of times the unit fraction fits into the whole. Encourage students to think of real-life examples where they might divide a whole into parts, like sharing a pizza among friends.

Understanding Unit Fractions – Definition of a unit fraction – A fraction with 1 as the top number – Examples: 1/2, 1/3, 1/4 – These are all unit fractions – Building fractions from units – Combine unit fractions to make others – Visualizing with fraction models – Use pie charts or bars to show units | Begin by explaining that a unit fraction is a type of fraction where the numerator (top number) is always 1. It represents one part of a whole that is divided into equal parts. Show examples of unit fractions like 1/2, 1/3, and 1/4 to illustrate the concept. Explain that all other fractions are composed of unit fractions added together; for instance, 3/4 is the same as 1/4 + 1/4 + 1/4. Use visual aids like pie charts or bar models to help students see how unit fractions make up other fractions. This foundational understanding will be crucial as they learn to divide whole numbers by unit fractions.

Visualizing Fractions with Models – Represent fractions with models – Use pie charts or bar models to visualize fractions – Explore unit fraction models – Unit fractions are fractions with 1 as the numerator – Learn to divide using models – See how models are split into equal parts to represent division – Practice with different models | This slide aims to help students visualize fractions by using models such as pie charts and bar models. By understanding that a unit fraction has a numerator of 1, students can better grasp the concept of dividing whole numbers by these fractions. Show students how to divide a model into equal parts to represent the division of a whole number by a unit fraction. Encourage them to practice with different models to solidify their understanding. Provide examples such as dividing a pie (whole) into equal slices (unit fractions) and explain how many slices (unit fractions) fit into a given number of pies (whole numbers).

Dividing Whole Numbers by Unit Fractions – Division: Splitting into equal parts – Dividing by a fraction equals multiplying by its reciprocal – If you have 1/3, the reciprocal is 3/1, or just 3 – Example: Dividing by 1/3 is multiplying by 3 – 6 ÷ 1/3 = 6 × 3 = 18 – Practice with real-world problems – How many 1/3-cup servings in 2 cups of rice? | This slide introduces the concept of dividing whole numbers by unit fractions. Start by explaining division as the process of splitting something into equal parts. Then, teach that dividing by a fraction is the same as multiplying by its reciprocal, which is flipping the numerator and denominator. Use the example of dividing by 1/3 to show that it’s the same as multiplying by 3. To reinforce the concept, provide real-world problems that involve dividing whole numbers by unit fractions, such as determining the number of servings in a recipe. This will help students understand and apply the concept in practical situations.

Dividing Whole Numbers by Unit Fractions – Visualizing division with models – Models make abstract concepts concrete – Using bar models for division – Bar models represent whole numbers and fractions – Example: Dividing 3 by 1/3 – How many 1/3-sized pieces fit into 3? | This slide introduces the concept of using visual models to understand the division of whole numbers by unit fractions. Models, such as bar models, help students to see the division process and make abstract concepts more concrete. For example, if we have a whole number 3 and we want to divide it by 1/3, we can use a bar model to represent the number 3 and then see how many segments of 1/3 fit into it. This visual approach is particularly effective for helping students grasp the concept of fraction division. Encourage students to draw their own bar models and to use them to solve different division problems involving unit fractions.

Let’s Practice Together: Division with Fractions – Practice: Divide 4 by 1/2 – Use visual aids like fraction bars or circles – Step-by-step model demonstration – Show dividing 4 into halves, how many halves in 4? – Discuss results with a classmate – Share your method and answer – Understand the outcome – Grasping ‘how many halves make a whole?’ | This slide is designed for a collaborative classroom activity where students will apply their understanding of dividing whole numbers by unit fractions. Begin with a clear example, using visual models such as fraction bars or pie charts to demonstrate how to divide 4 by 1/2. Walk the students through each step, ensuring they understand the concept of how many times 1/2 fits into 4. After the demonstration, students should pair up to discuss their understanding and the result of the division. This peer interaction will help solidify their comprehension. Conclude with a group discussion to address any misconceptions and to reinforce the concept that dividing by a fraction is the same as multiplying by its reciprocal. Provide additional practice problems for students to work on individually or in pairs.

Your Turn to Try: Division with Models – Practice dividing whole numbers by fractions – Work in pairs on problems – Use models to divide – Draw a model to represent the division – Share your model and solution – Explain how you used the model to find the answer | This slide is an interactive activity for students to apply their understanding of dividing whole numbers by unit fractions using models. Students should be paired up and given practice problems where they will use visual models, such as fraction bars or circles, to divide whole numbers by unit fractions. Encourage them to discuss their strategies with their partner and to draw their models on paper. After completing the problems, each pair will present their model and explain the process they used to find the answer. This will help solidify their understanding and allow for peer learning. Possible activities could include dividing a number of objects into fractional parts, using grid paper to visualize division, or creating story problems that involve division of whole numbers by unit fractions.

Class Activity: Model Division with Crafts – Create a physical division model – Use craft materials for building – Use items like paper, beads, or blocks – Show division by a unit fraction – Example: How many 1/4 pieces in 2? – Explain your model to the class | This activity is designed to help students visualize the concept of dividing whole numbers by unit fractions. Provide a variety of craft materials such as colored paper, beads, or building blocks. Students will use these materials to construct a model that represents a division problem involving a whole number and a unit fraction. For instance, they could show how many 1/4 pieces can be made from 2 whole items. Encourage creativity and ensure they understand that the unit fraction is the size of the piece, and the whole number is how many times that piece fits into the whole. After building their models, students will present and explain their division to the class, reinforcing their understanding through teaching. Prepare to guide them with questions and provide additional examples if needed.

Conclusion: Dividing Whole Numbers by Unit Fractions – Recap: Division by unit fractions – Remember, dividing by a fraction is like multiplying by its reciprocal. – Importance of this concept – Helps in understanding real-world problems like splitting a pizza. – Preview: Dividing fractions by fractions – Next, we’ll learn how to divide a fraction by another fraction. – Encourage practice at home | As we wrap up today’s lesson, it’s crucial to revisit the main points of dividing whole numbers by unit fractions. Emphasize the method of multiplying by the reciprocal to find the answer. Discuss how this concept applies to everyday situations, such as dividing a single item among a group, which helps solidify the practicality of the lesson. Looking ahead, give the students a sneak peek into the next lesson where they will build on this foundation to tackle dividing fractions by fractions. Encourage them to practice at home with different examples to gain confidence. Provide a few practice problems for them to take home and remind them that understanding these concepts will greatly enhance their math skills.

Homework: Dividing Whole Numbers by Unit Fractions – Complete the division worksheet – Create your own division problems – Think of real-life scenarios like sharing pizza – Solve the problems you created – Use models or draw pictures to help solve – Get ready to discuss in class | This homework assignment is designed to reinforce students’ understanding of dividing whole numbers by unit fractions. The worksheet provides structured practice, while creating their own problems encourages deeper engagement with the concept. Encourage students to think of practical situations where they might divide a whole into parts, such as sharing food or distributing items evenly. Remind them to use visual models like fraction circles or number lines if they’re struggling to solve the problems. Next class, we’ll have a discussion where students can explain their reasoning and the strategies they used, which will help consolidate their learning and build confidence.