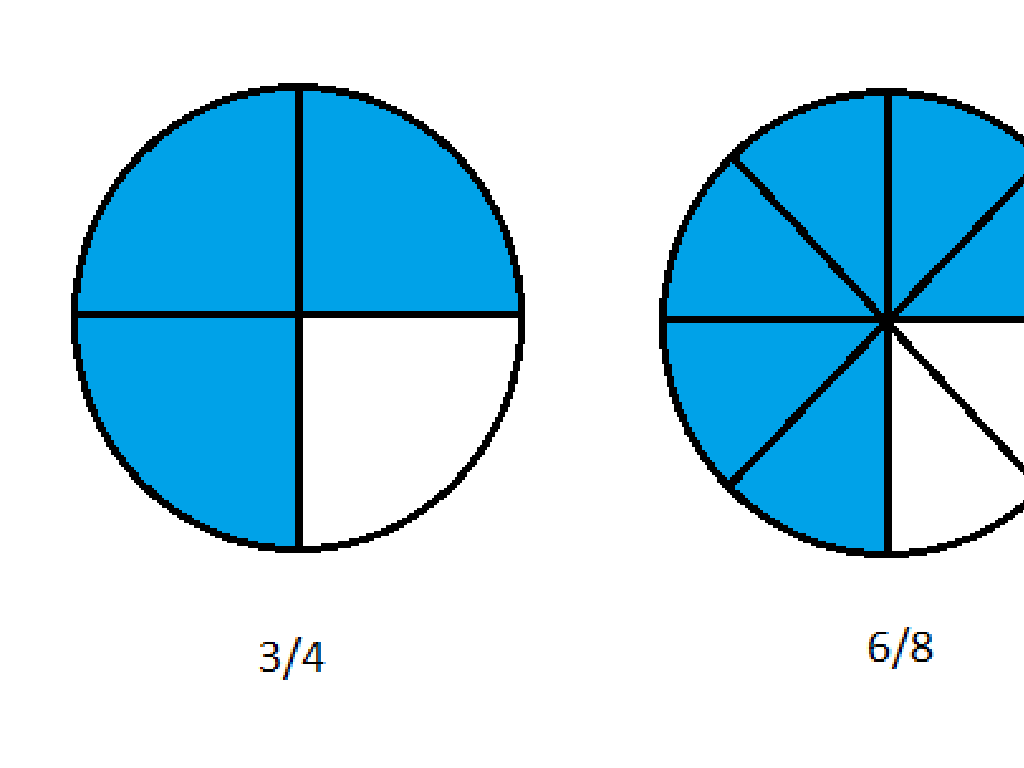Your next great Lessn starts here.

Welcome to Fractions! – Learn what fractions are – Fractions as parts of a whole – Imagine slicing a pizza into equal parts – Matching fractions with models – Use shapes divided into equal parts to visualize – Practice with fun activities – We’ll use fraction circles and bars in class | This slide introduces the concept of fractions to third-grade students. Begin by explaining that a fraction represents a part of a whole, just like a slice of pizza is a part of an entire pizza. Use visual aids like fraction circles or bars to help students match fractions to models, reinforcing the idea that fractions are equal parts of a whole. Engage the students with hands-on activities where they can practice matching fractions to different models, ensuring they understand the concept. Encourage participation and provide positive feedback to build their confidence in learning about fractions.

What is a Fraction? – A fraction shows part of a whole – Like a slice of pizza from a whole pie – Top number is the numerator – It tells how many pieces we’re looking at – Bottom number is the denominator – It shows into how many slices the pizza is cut – Numerator counts the parts we have – If we have 2 slices, numerator is 2 | Begin by explaining that a fraction is a way to represent a part of something that is whole, using the example of a pizza cut into slices. The top number, or numerator, indicates the number of slices we have, while the bottom number, or denominator, shows how many slices the pizza was originally cut into. Use visual aids like a circle (pizza) divided into equal parts to illustrate this concept. Encourage students to think of fractions in terms of everyday items to make the concept more relatable and easier to grasp. Practice with different fractions to show how the numerator and denominator change with different amounts of the whole.

Fraction Models: Visualizing Fractions – Models make fractions easy to see – Explore circles, bars, and sets – Circles (like pizzas), bars (like chocolate bars), and sets (like a dozen eggs) – Divide each model into equal parts – If a circle is a pizza, we cut it into equal slices to show fractions – Matching fractions with models | This slide introduces students to the concept of using visual models to understand fractions. Models are a concrete way for students to grasp the abstract concept of fractions. Introduce the three types of models: circles, bars, and sets, and explain that each can represent fractions by being divided into equal parts. For example, a circle (pizza) can be cut into equal slices, a bar (chocolate bar) can be broken into equal pieces, and a set (a dozen eggs) can be grouped into smaller equal sets. Encourage students to think of these models when trying to visualize fractions in real life. The goal is for students to be able to match given fractions to the correct representation using these models.

Matching Fractions to Models – Determine total equal parts – If a pizza is cut into 8 pieces, the total parts is 8. – Count shaded parts for numerator – If 3 pieces of the pizza are eaten, the numerator is 3. – Write the fraction represented – With 3 out of 8 pieces eaten, the fraction is 3/8. | This slide is aimed at helping third-grade students understand how to match fractions to visual models. Begin by explaining that the total number of equal parts in a model gives us the denominator of the fraction. Then, show how counting the shaded (or filled) parts gives us the numerator. Finally, demonstrate how to write the fraction by placing the numerator over the denominator. Use simple, relatable examples like slices of pizza or pieces of a chocolate bar to illustrate these concepts. Encourage students to practice with different models and to create their own examples for peer review.

Matching Fractions to Models – Example 1: Pizza pieces – A pizza cut into 4 equal parts, 1 part eaten – Fraction of pizza left – 3 out of 4 pieces remain, so 3/4 of the pizza is left – Example 2: Colored balls – 8 balls in total, 2 of which are red – Fraction of red balls – 2 out of 8 balls are red, so the fraction is 2/8 | This slide is designed to help students visualize fractions through relatable examples. Start with a pizza model, explaining that each piece represents a fraction of the whole. After one piece is eaten, ask students to identify the fraction of the pizza that remains. For the second example, use a model with balls of different colors to represent fractions. Explain that the total number of balls is the denominator, while the number of red balls is the numerator. These examples will help students understand how fractions represent parts of a whole in a concrete way. Encourage students to draw their own models and come up with similar examples.

Your Turn to Match: Fractions with Models – Observe the provided models – Write the fractions they represent – Look at each shaded part to determine the fraction – Be ready to discuss your answers – Share with the class – Explain how you figured out the fractions | This slide is an interactive class activity designed to help students practice matching fractions to visual models. Provide students with various models that visually represent fractions, such as pie charts, bar models, or number lines with parts shaded. Encourage them to carefully observe the shaded parts and write down the corresponding fraction for each model. Remind them to consider both the numerator, representing the shaded parts, and the denominator, representing the total number of equal parts. After they have written down the fractions, facilitate a class discussion where students can share their answers and explain their thought process. This activity will reinforce their understanding of fractions and provide an opportunity for peer learning.

Class Activity: Fraction Bingo – Receive your Fraction Bingo card – Listen as fractions are called out – Match fractions to your card – Use the models on your card to find the called fraction – Aim for five in a row to win! | This interactive activity is designed to help students recognize and match fractions using visual models. Each student will receive a Bingo card with different fraction models on it. As the teacher calls out fractions, students will look for a corresponding fraction model on their card. This exercise will reinforce their understanding of fractions as parts of a whole and how to identify them visually. Prepare several sets of Bingo cards with various fraction models and ensure that each card is unique to make the game fair. Have small prizes ready for the winners to make the activity exciting. Possible variations of the activity could include having students call out the fractions for extra speaking practice, or using different shapes and models to represent the fractions.