Your next great Lessn starts here.

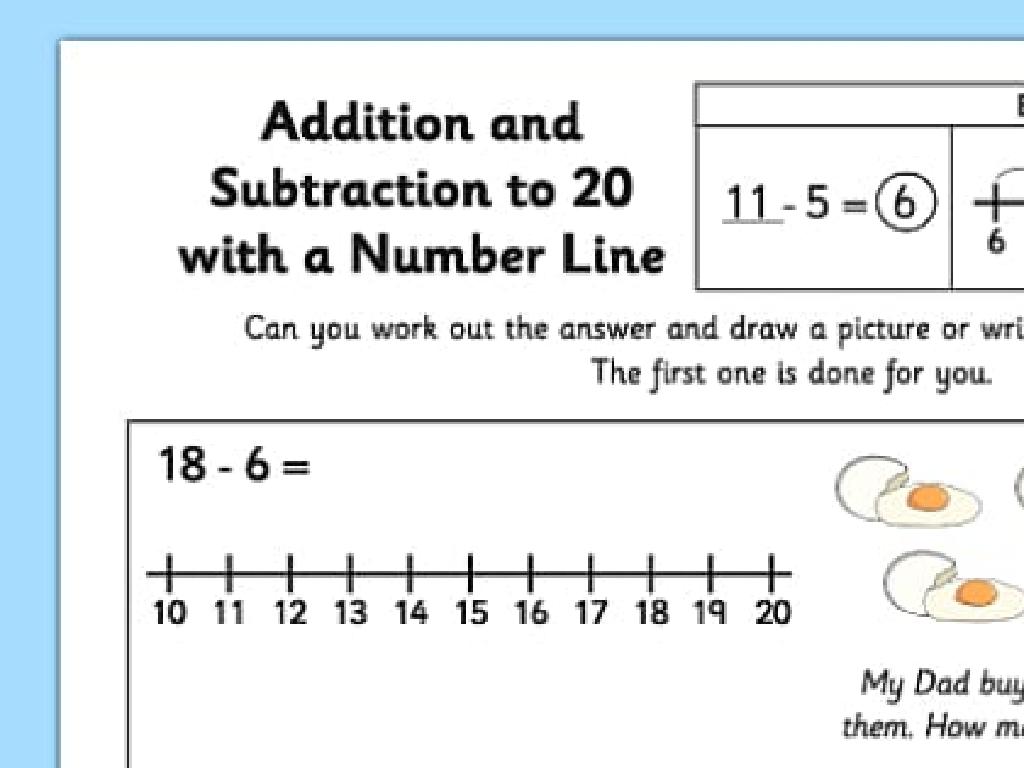
Graph Patterns Using Rules – Explore graph patterns today – Learn about variable expressions – Variables represent numbers in expressions, like ‘n’ in 2n+3 – Discover how to predict patterns – Use rules to find what comes next in a pattern – Practice with fun activities – We’ll graph patterns and see how they change | This slide introduces students to the concept of graphing patterns using rules and understanding variable expressions. Begin by explaining that a variable is a symbol that stands for a number we don’t know yet. Show how variable expressions can help us describe and predict patterns. For example, if we have a pattern of numbers that increases by 2 each time, we can write this as ‘2n’ where ‘n’ is the position in the pattern. Engage the students with examples and encourage them to participate in predicting the next numbers in different patterns. Conclude with hands-on activities where students can apply rules to graph patterns and visually see the relationship between the numbers in a sequence.

Understanding Variables in Math – Variables are like boxes for numbers – Symbols representing any number – Think of a variable as a placeholder – Commonly use letters like x, y, z – For example, x can be 1, 2, 3, or any number – Variables in math equations – We use them to write rules for patterns | This slide introduces the concept of variables to fifth-grade students. Begin by explaining that a variable is like an empty box where we can put any number we want. It’s a symbol, usually a letter, that takes the place of a number we might not know yet or that can change. Common letters used as variables are x, y, and z. Emphasize that variables are essential in math because they allow us to write expressions and equations that represent patterns and rules. Use simple examples to show how variables work and how they can represent different values in different situations. Encourage students to think of variables as a fun way to explore numbers and patterns.

Understanding Expressions in Math – Expressions combine numbers and variables – Like a recipe, mixing ingredients to create something new – They can have +, -, *, and / – Operations tell us how to mix these ‘ingredients’ – Example: 3x + 2, where x is variable – If x=2, then 3x + 2 becomes 3*2 + 2 = 8 – Expressions represent values – They don’t have an equal sign like equations do | This slide introduces the concept of expressions in mathematics, which are fundamental to understanding variable expressions. Expressions are like recipes that tell us how to combine different ‘ingredients’ or numbers and variables using operations such as addition, subtraction, multiplication, and division. Use the example 3x + 2 to show how a variable, x, can change the value of the expression. Emphasize that expressions are not complete sentences like equations; they don’t have an equal sign. Encourage students to think of expressions as unfinished math problems that represent a value. Have them practice creating their own expressions using different numbers and variables.

Creating Rules for Patterns – Rules reveal and predict patterns – Think of rules as expression instructions – Example: Start with 2, add 4 each step – If we begin at 2, our sequence is 2, 6, 10, 14… – Practice creating your own rules – Try with different starting numbers and increments | This slide introduces the concept of using rules to identify and predict patterns in sequences. Rules in mathematics help us understand how sequences are formed and how to find subsequent numbers. For example, if we start with the number 2 and add 4 each time, we get a sequence where each number is 4 more than the previous one. Encourage students to create their own rules by choosing a starting number and deciding how much to add or subtract to form a pattern. This exercise will help them grasp the concept of variable expressions and how they can be applied to find patterns.

Graphing Patterns with Rules – Graphs visualize rules – Rules and expressions become visual aids, like a picture book of math. – Points represent pattern steps – Each dot on the graph is a part of the story, showing the sequence. – Point patterns reveal rules – Just like connecting dots, the layout of points can show us the pattern’s rule. – Practice with different rules | This slide introduces students to the concept of graphing patterns using rules. Start by explaining that graphs turn abstract rules and expressions into visual representations that are easier to understand. Each point on the graph corresponds to a step in the pattern, and by looking at the overall arrangement of these points, students can begin to identify the underlying rule. Encourage students to practice plotting points on a graph using different rules to see how the pattern changes with each rule. This will help them understand the relationship between mathematical expressions and their graphical representations.

Let’s Practice Graphing Patterns! – Start with zero and add 3 – Plot points: 0, 3, 6, 9, 12 – On the graph, mark the points (0,0), (1,3), (2,6), (3,9), (4,12) – Observe the pattern formed – Do the points line up? What’s the spacing between them? – Discuss the pattern’s features – Are the points forming a straight line? What does this tell us about the rule? | This slide is an interactive class activity designed to help students understand how to graph patterns using rules. Begin by explaining the rule ‘Add 3’ starting with the number 0. Have students plot the points on a graph as you go through the sequence together. Encourage them to look for and discuss the pattern that emerges. They should notice that the points form a straight line, indicating a constant rate of change. This activity will help them visualize how arithmetic sequences can be represented graphically and understand the concept of a linear pattern. Possible variations for individual practice could include changing the starting number or the rule (e.g., ‘Add 4’ or ‘Subtract 2’).

Your Turn: Create a Rule – Think of a simple rule – Write an expression using your rule – Example: Add 2 to each number starting at 1 (1, 3, 5, 7…) – Plot points using the expression – If your rule is +2, plot (1,3), (2,5), (3,7)… – Observe the pattern on the graph – Does your graph show a straight line? | This activity slide encourages students to apply their understanding of variable expressions by creating their own rules. Students should think of a simple mathematical rule, such as adding or subtracting a consistent number. They will then write a variable expression that represents their rule. Using this expression, students will plot points on a graph to visualize the pattern their rule creates. This hands-on activity helps solidify the concept of variable expressions and their graphical representations. Teachers should circulate the room to assist students in plotting and to facilitate discussions about the patterns they observe. Possible variations of the activity could include using different operations or starting points to see how the graph changes.

Class Activity: Graph the Pattern – In groups, pick a rule for the pattern – Create a graph based on your rule – Use graph paper and markers to draw – Present your graph to the class – Explain how you used the rule to make the graph – Can classmates guess your rule? – Think about what made your rule easy or hard to guess | This activity is designed to help students understand the concept of graphing patterns using rules. Divide the class into small groups and have each group select a rule, such as ‘add 2’ or ‘subtract 1’. They will then use this rule to create a sequence and graph it on graph paper. Once completed, each group will present their graph to the class and explain the rule they used. Encourage the audience to guess the rule based on the pattern observed in the graph. This will foster a deeper understanding of how rules apply to patterns and how they can be visually represented through graphs. Possible variations for the activity could include using different types of rules, such as multiplying or dividing, to show how these operations affect the slope of the graphed line.

Conclusion: The Power of Patterns – Celebrating our graphing skills – Variable expressions in daily life – Variables help predict outcomes, like savings over time. – Recognizing everyday patterns – Think of patterns like the days of the week or traffic lights. – Reflect on what we’ve learned | As we wrap up our lesson on graphing patterns using rules, it’s important to reflect on the significance of what we’ve learned. Understanding variable expressions is not just a math skill; it’s a tool we use in everyday life to make predictions and understand the world around us. Encourage students to identify patterns they encounter daily, such as the progression of seasons or the routine of a school day. This helps them see the relevance of math beyond the classroom. Ask them to share examples and discuss how recognizing these patterns can help with planning and decision-making. Celebrate their achievements in mastering graphing skills and encourage them to continue observing patterns in their environment.